Page cover

🚗1. 矢量分析

1.1 矢量代数

1.1.1 标量和矢量

标量只有大小，矢量既有大小也有方向

常矢量：方向和大小都不变的矢量

在三维坐标系中，矢量可以用坐标分量来表示：

A⃗=Axe⃗x+Aye⃗y+Aze⃗z\vec{A}=A_x\vec{e}_x+A_y\vec{e}_y+A_z\vec{e}_z

其中，

Ax=Acos⁡αAy=Acos⁡βAz=Acos⁡γA_x=A\cos\alpha\\ A_y=A\cos\beta\\ A_z=A\cos\gamma

因此：

A⃗=A(e⃗xcos⁡α+e⃗ycos⁡β+e⃗zcos⁡γ)\begin{aligned} \vec{A}=A(\vec{e}_x\cos\alpha+\vec{e}_y\cos\beta+\vec{e}_z\cos\gamma) \end{aligned}

向量A⃗\vec{A}方向的单位向量为

e⃗A=e⃗xcos⁡α+e⃗ycos⁡β+e⃗zcos⁡γ\vec{e}_A=\vec{e}_x\cos\alpha+\vec{e}_y\cos\beta+\vec{e}_z\cos\gamma

图示：

1.1.2 矢量的代数运算

  1. 矢量的加减法

    两矢量的加减在几何上是以这两矢量为邻边的平行四边形的对角线，如图

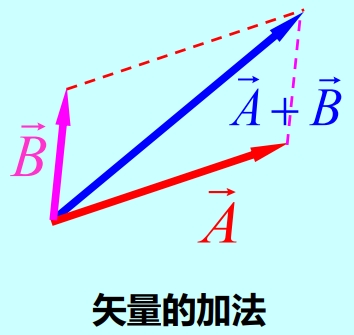
    Image 1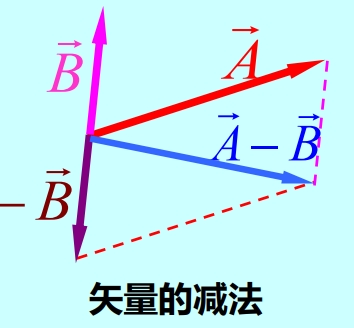
    Image 2

    在直角坐标系中两矢量的加减法：

    A⃗±B⃗=e⃗x(Ax±Bx)+e⃗y(Ay±By)+e⃗z(Az±Bz)\vec{A}\pm\vec{B}=\vec{e}_x(A_x\pm B_x)+\vec{e}_y(A_y\pm B_y)+\vec{e}_z(A_z\pm B_z)

    矢量的加减符合交换律和结合律：

    交换律 A⃗+B⃗=B⃗+A⃗结合律 A⃗+(B⃗+C⃗)=(A⃗+B⃗)+C⃗\begin{align*} &交换律 \: \vec{A}+\vec{B}=\vec{B}+\vec{A}\\ &结合律 \: \vec{A}+(\vec{B}+\vec{C})=(\vec{A}+\vec{B})+\vec{C} \end{align*}

  2. 标量乘矢量

    kA⃗=e⃗xkAx+e⃗ykAy+e⃗zkAzk\vec{A}=\vec{e}_xkA_x+\vec{e}_ykA_y+\vec{e}_zkA_z

  3. 矢量的点积

    A⃗⋅B⃗=ABcos⁡θ=AxBx+AyBy+AzBz\vec{A}\cdot\vec{B}=AB\cos\theta=A_xB_x+A_yB_y+A_zB_z

    矢量的点积符合交换律：

    A⃗⋅B⃗=B⃗⋅A⃗\vec A\cdot\vec B=\vec B\cdot\vec A

    矢量的点积相当于一个矢量和另一个矢量在该矢量方向上投影的乘积，两矢量垂直时点积为0，平行时点积为模的乘积

  4. 矢量的叉积 矢量的叉积定义为

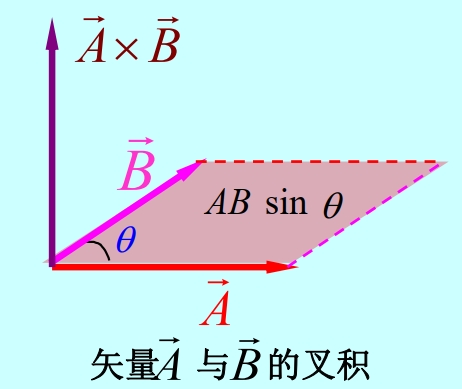
    A⃗×B⃗=e⃗nABsin⁡θ\vec{A}\times\vec{B}=\vec{e}_nAB\sin\theta

    在直角坐标系中可写成行列式的形式：

    A⃗×B⃗=∣e⃗xe⃗ye⃗zAxAyAzBxByBz∣\vec{A}\times\vec{B}=\begin{vmatrix}\vec{e}_x&\vec{e}_y&\vec{e}_z\\A_x&A_y&A_z\\B_x&B_y&B_z\end{vmatrix}

    将该行列式按第一行展开，可得：

    A⃗×B⃗=e⃗x(AyBz−AzBy)+e⃗y(AzBx−AxBz)+e⃗z(AxBy−AyBx)\vec{A}\times\vec{B}=\vec{e}_x(A_yB_z-A_zB_y)+\vec{e}_y(A_zB_x-A_xB_z)+\vec{e}_z(A_xB_y-A_yB_x)

    叉积的方向由右手螺旋定则决定，因此由

    A⃗×B⃗=−B⃗×A⃗\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}

    两种特殊情况：

    若 A⃗⊥B⃗,则 ∣A⃗×B⃗∣=AB若 A⃗//B⃗,则 ∣A⃗×B⃗∣=0\begin{aligned}&\textbf{若 }\vec{A}\perp\vec{B}\text{,则 }\left|\vec{A}\times\vec{B}\right|=AB\\&\textbf{若 }\vec{A}//\vec{B}\text{,则 }\left|\vec{A}\times\vec{B}\right|=0\end{aligned}

  5. 矢量的混合运算

    • 分配律：(A⃗+B⃗)⋅C⃗=A⃗⋅C⃗+B⃗⋅C⃗(\vec{A}+\vec{B})\cdot\vec{C}=\vec{A}\cdot\vec{C}+\vec{B}\cdot\vec{C}

    • 分配律：(A⃗+B⃗)×C⃗=A⃗×C⃗+B⃗×C⃗(\vec{A}+\vec{B})\times\vec{C}=\vec{A}\times\vec{C}+\vec{B}\times\vec{C}

    • 标量三重积：A⃗⋅(B⃗×C⃗)=B⃗⋅(C⃗×A⃗)=C⃗⋅(A⃗×B⃗)\vec{A}\cdot(\vec{B}\times\vec{C})=\vec{B}\cdot(\vec{C}\times\vec{A})=\vec{C}\cdot(\vec{A}\times\vec{B})

    • 矢量三重积：A⃗×(B⃗×C⃗)=(A⃗⋅C⃗)B⃗−(A⃗⋅B⃗)C⃗\vec A\times(\vec B\times\vec C)=(\vec A\cdot\vec C)\vec B-(\vec A\cdot\vec B)\vec C

    标量三重积的证明：

    已知A⃗=Axe⃗x+Aye⃗y+Aze⃗z,B⃗=Bxe⃗x+Bye⃗y+Bze⃗z,C⃗=Cxe⃗x+Cye⃗y+Cze⃗z\vec{A}=A_x\vec{e}_x+A_y\vec{e}_y+A_z\vec{e}_z,\vec{B}=B_x\vec{e}_x+B_y\vec{e}_y+B_z\vec{e}_z,\vec{C}=C_x\vec{e}_x+C_y\vec{e}_y+C_z\vec{e}_z，可得

    A⃗⋅(B⃗×C⃗)=∣AxAyAzBxByBzCxCyCz∣\vec{A}\cdot(\vec{B}\times\vec{C})= \begin{vmatrix} A_x&A_y&A_z\\ B_x&B_y&B_z\\ C_x&C_y&C_z\\ \end{vmatrix}

    证明如下：

    A⃗⋅(B⃗×C⃗)=(Axe⃗x+Aye⃗y+Azez⃗)⋅(ex⃗∣ByBzCyCz∣−ey⃗∣AxCzAxCz∣+ez⃗∣AxByAxBy∣)=∣AxAyAzBxByBzCxCyCz∣\begin{align*} \vec{A}\cdot(\vec{B}\times\vec{C})=& (A_x\vec{e}_x+A_y\vec{e}_y+A_z\vec{e_z})\cdot(\vec{e_x} \begin{vmatrix} B_y&B_z\\ C_y&C_z\\ \end{vmatrix}- \vec{e_y}\begin{vmatrix} A_x&C_z\\ A_x&C_z\\ \end{vmatrix}+ \vec{e_z}\begin{vmatrix} A_x&B_y\\ A_x&B_y\\ \end{vmatrix})\\ =& \begin{vmatrix} A_x&A_y&A_z\\ B_x&B_y&B_z\\ C_x&C_y&C_z\\ \end{vmatrix} \end{align*}

    由行列式的性质，我们可知，当顺序不变，改变A⃗、B⃗、C⃗\vec{A}、\vec{B}、\vec{C}的位置也不会影响标量三重积的结果，也可以重新证一次B⃗⋅(C⃗×A⃗)\vec{B}\cdot(\vec{C}\times\vec{A})，得：

    A⃗⋅(B⃗×C⃗)=B⃗⋅(C⃗×A⃗)=C⃗⋅(A⃗×B⃗)\vec{A}\cdot(\vec{B}\times\vec{C})=\vec{B}\cdot(\vec{C}\times\vec{A})=\vec{C}\cdot(\vec{A}\times\vec{B})

    几何意义为一个平行六面体的体积

矢量三重积的证明：

首先为了方便记忆可以使用”BAC-CAB（BACK-CAB，后面的出租车）“的口诀。一种比较另类的证明方式：

对A⃗×(B⃗×C⃗)\vec A\times(\vec B\times\vec C)而言，B⃗×C⃗\vec B\times\vec C将得到B⃗\vec{B}向量和C⃗\vec{C}向量所在平面的法向量n⃗\vec{n}，n⃗\vec{n}与A⃗\vec{A}叉积所得向量必处于B⃗\vec{B}和C⃗\vec{C}所在平面，则可表示为：

A⃗×(B⃗×C⃗)=pB⃗+qC⃗\vec A\times(\vec B\times\vec C)=p\vec{B}+q\vec{C}

此时的A⃗\vec{A}向量与其也是垂直关系，点积则有：

A⃗⋅(pB⃗+qC⃗)=pA⃗B⃗+qA⃗C⃗\vec{A}\cdot(p\vec{B}+q\vec{C})=p\vec{A}\vec{B}+q\vec{A}\vec{C}

若要等式恒成立，又考虑到pp和qq是常数，则pp必然等于A⃗\vec{A}和C⃗\vec{C}的点积，qq必然等于A⃗\vec{A}和B⃗\vec{B}的点积的负数，则有：

A⃗×(B⃗×C⃗)=(A⃗⋅C⃗)B⃗−(A⃗⋅B⃗)C⃗\vec A\times(\vec B\times\vec C)=(\vec A\cdot\vec C)\vec B-(\vec A\cdot\vec B)\vec C

1.2 三种常用的正交曲线坐标系

三维空间任意一点的位置可通过三条相互正交曲线的交点来确定，三条正交曲线组成的确定三维空间任意点位置的体系，称为正交曲线坐标系，三条曲线称为坐标轴，描述坐标轴的量称为坐标变量，在电磁场与电磁波中，三种常用的正交曲线坐标系为：直角坐标系，圆柱坐标系，球面坐标系。

1.2.1 直角坐标系

Image 1
Image 2

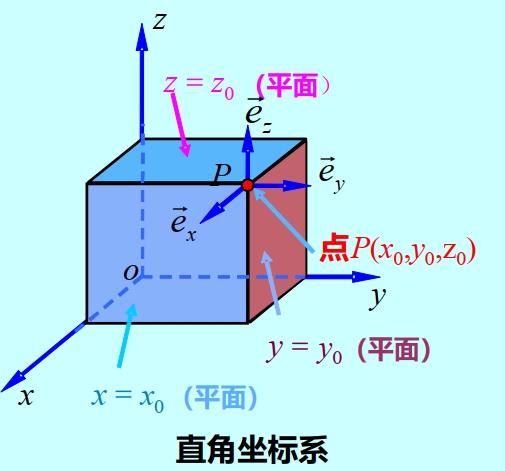
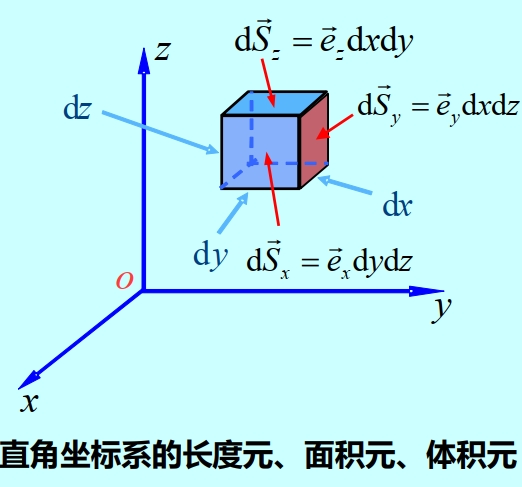
在直角坐标系中，三个坐标变量为：

x、y、zx、y、z

它们的变化范围为：

−∞<x<∞,−∞<y<∞,−∞<z<∞-\infty<x<\infty ,-\infty<y<\infty ,-\infty<z<\infty

坐标单位矢量为：

e⃗x,e⃗y,e⃗z\vec{e}_x,\vec{e}_y,\vec{e}_z

任意矢量A⃗\vec A在直角坐标系中可表示为：

A⃗=ex⃗Ax+ey⃗Ay+ez⃗Az\vec{A}=\vec{e_x}A_x+\vec{e_y}A_y+\vec{e_z}A_z

其中AxA_x、AyA_y和AzA_z分别是矢量A⃗\vec{A}在ex⃗\vec{e_x}、ey⃗\vec{e_y}和ez⃗\vec{e_z}方向上的投影 从坐标原点出发的矢量r⃗\vec r表示空间任一点的位置，称为位置矢量，在直角坐标系中，位置矢量

r⃗=e⃗xx+e⃗yy+e⃗zz\vec{r}=\vec{e}_xx+\vec{e}_yy+\vec{e}_zz

其微分矢量，又叫线元矢量为

dl⃗=e⃗xdx+e⃗ydy+e⃗zdz\mathrm{d}\vec{l}=\vec{e}_x\mathrm{d}x+\vec{e}_y\mathrm{d}y+\vec{e}_z\mathrm{d}z

与三个坐标单位矢量相垂直的三个面积元分别为：

dS⃗x=e⃗xdlydlz=e⃗xdydzdS⃗y=e⃗ydlxdlz=e⃗ydxdzdS⃗z=e⃗zdlxdly=e⃗zdxdy\begin{gathered} \mathrm{d}\vec{S}_{x}=\vec{e}_{x}\mathrm{d}l_{y}\mathrm{d}l_{z}=\vec{e}_{x}\mathrm{d}y\mathrm{d}z \\ \mathrm{d}\vec{S}_y=\vec{e}_y\mathrm{d}l_x\mathrm{d}l_z=\vec{e}_y\mathrm{d}x\mathrm{d}z \\ \mathrm{d}\vec{S}_{z}=\vec{e}_{z}\mathrm{d}l_{x}\mathrm{d}l_{y}=\vec{e}_{z}\mathrm{d}x\mathrm{d}y \end{gathered}

体积元为：

dV=dxdydz\mathrm{d}V=\mathrm{d}x\mathrm{d}y\mathrm{d}z

1.2.2 圆柱坐标系

Image 1
Image 2

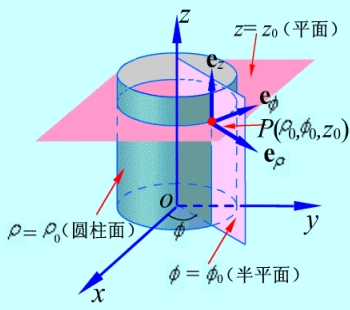
圆柱坐标系的三个坐标变量为：

ho,ϕ,zho,\phi,z

它们的变化范围为：

0≤ρ<∞,0≤ϕ≤2π,−∞<z<∞0\leq\rho<\infty,0\leq\phi\leq2\pi,-\infty<z<\infty

圆柱坐标系与直角坐标系之间的变换关系为：

ho=x2+y2,ϕ=arctan⁡(y/x),z=zho=\sqrt{x^2+y^2} ,\phi=\arctan( y/x ) ,z=z

坐标单位矢量为：

e⃗ρ,e⃗ϕ,e⃗z\vec{e}_\rho,\vec{e}_\phi,\vec{e}_z

它们的方向是ρ、ϕ\rho、\phi和zz的增加的方向且遵循右手螺旋法则，如图

由此可得

eρ⃗=ex⃗cos⁡ϕ+ey⃗sin⁡ϕ,eϕ⃗=−ex⃗sin⁡ϕ+ey⃗cos⁡ϕ\vec{e_\rho}=\vec{e_x}\cos\phi+\vec{e_y}\sin\phi,\vec{e_\phi}=-\vec{e_x}\sin\phi+\vec{e_y}\cos\phi

写成矩阵的形式为：

[eρeϕez]=[cos⁡ϕsin⁡ϕ0−sin⁡ϕcos⁡ϕ0001][exeyez]\begin{bmatrix}\boldsymbol{e}_\rho\\\boldsymbol{e}_\phi\\\boldsymbol{e}_z\end{bmatrix}=\begin{bmatrix}\cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{bmatrix}\begin{bmatrix}\boldsymbol{e}_x\\\boldsymbol{e}_y\\\boldsymbol{e}_z\end{bmatrix}

在圆柱坐标系中，坐标矢量eρ⃗\vec{e_\rho}和eϕ⃗\vec{e_\phi}都表示常矢量，都是随ϕ\phi变化的，且

{∂eρ∂ϕ=−exsin⁡ϕ+eycos⁡ϕ=eϕ∂eϕ∂ϕ=−excos⁡ϕ−eysin⁡ϕ=−eρ\begin{cases}\frac{\partial\boldsymbol{e}_\rho}{\partial\boldsymbol{\phi}}=-\boldsymbol{e}_x\sin\boldsymbol{\phi}+\boldsymbol{e}_y\cos\boldsymbol{\phi}=\boldsymbol{e}_\phi\\\\\frac{\partial\boldsymbol{e}_\phi}{\partial\boldsymbol{\phi}}=-\boldsymbol{e}_x\cos\boldsymbol{\phi}-\boldsymbol{e}_y\sin\boldsymbol{\phi}=-\boldsymbol{e}_\rho\end{cases}

不同点的eρ⃗\vec{e_\rho}和eϕ⃗\vec{e_{\phi}}一般是不同的，因此不同点的两个矢量一般不能直接进行加法和乘法运算。

在圆柱坐标系中，位置矢量为

r⃗=e⃗ρρ+e⃗zz\vec{r}=\vec{e}_\rho\rho+\vec{e}_zz

其微分元矢量即线元矢量为：

dl⃗=e⃗ρdρ+e⃗ϕρdϕ+e⃗zdz\mathrm{d}\vec{l}=\vec{e}_\rho\mathrm{d}\rho+\vec{e}_\phi\rho\mathrm{d}\phi+\vec{e}_z\mathrm{d}z

dlρdl_\rho、dlϕdl_\phi和dlzdl_z与各自坐标变量的微分之比称为度量系数（或拉梅系数），分别用hρ、hϕh_\rho、h_\phi和hzh_z表示，则

hρ=dlρdρ=1,hϕ=dlϕdϕ=ρ,hz=dlzdz=1h_\rho=\frac{\mathrm{d}l_\rho}{\mathrm{d}\rho}=1 ,h_\phi=\frac{\mathrm{d}l_\phi}{\mathrm{d}\phi}=\rho ,h_z=\frac{\mathrm{d}l_z}{\mathrm{d}z}=1

在圆柱坐标系中与三个坐标单位矢量相垂直的三个面积元分别为：

dS⃗ρ=e⃗ρdlϕdlz=e⃗ρρdϕdzdS⃗ϕ=e⃗ϕdlρdlz=e⃗ϕdρdzdS⃗z=e⃗zdlρdlϕ=e⃗zρdρdϕ\mathrm{d}\vec{S}_{\rho}=\vec{e}_{\rho}\mathrm{d}l_{\phi}\mathrm{d}l_{z}=\vec{e}_{\rho}\rho\mathrm{d}\phi\mathrm{d}z\\\mathrm{d}\vec{S}_{\phi}=\vec{e}_{\phi}\mathrm{d}l_{\rho}\mathrm{d}l_{z}=\vec{e}_{\phi}\mathrm{d}\rho\mathrm{d}z\\\mathrm{d}\vec{S}_{z}=\vec{e}_{z}\mathrm{d}l_{\rho}\mathrm{d}l_{\phi}=\vec{e}_{z}\rho\mathrm{d}\rho\mathrm{d}\phi

体积元为：

dV=ρdρdϕdz\mathrm{d}V=\rho\mathrm{d}\rho\mathrm{d}\phi\mathrm{d}z

1.2.3 球坐标系

Image 1
Image 2

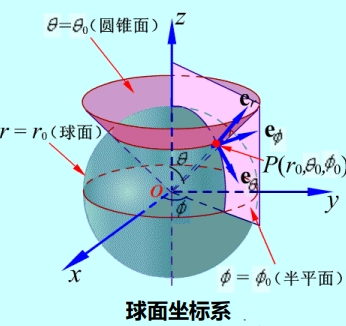
球坐标系的三个坐标变量为

r,θ,ϕr,\theta,\phi

它们的变化范围为：

0⩽r<∞,0⩽θ⩽π,0⩽ϕ⩽2π0\leqslant r<\infty ,0\leqslant\theta\leqslant\pi ,0\leqslant\phi\leqslant2\pi

球坐标系和直角坐标系的变换关系为：

r=x2+y2+z2,θ=arccos⁡(z/x2+y2+z2),ϕ=arctan⁡(y/x)r=\sqrt{x^2+y^2+z^2} ,\theta=\arccos\left( z/\sqrt{x^2+y^2+z^2} \right) ,\phi=\arctan\left( y/x \right)

坐标单位矢量为：

er⃗,eθ⃗,eϕ⃗\vec{e_r},\vec{e_\theta},\vec{e_{\phi}}

它们的方向分别是该点r、θr、\theta和ϕ\phi增加的方向。

球坐标系的坐标变量和直角坐标系的坐标变量的变换关系为：

[ereθeϕ]=[sin⁡θcosϕsin⁡θsinϕcos⁡θcos⁡θcosϕcos⁡θsinϕ−sin⁡θ−sin⁡ϕcos⁡ϕ0][exeyez]\begin{bmatrix}e_r\\\\e_\theta\\\\e_\phi\end{bmatrix}=\begin{bmatrix}\sin\theta\mathrm{cos}\phi&\sin\theta\mathrm{sin}\phi&\cos\theta\\\\\cos\theta\mathrm{cos}\phi&\cos\theta\mathrm{sin}\phi&-\sin\theta\\\\-\sin\phi&\cos\phi&0\end{bmatrix}\begin{bmatrix}e_x\\\\e_y\\\\e_z\end{bmatrix}

在球坐标系中，坐标单元矢量er、eθe_r、e_\theta和eϕe_\phi都不是常矢量，且

{∂er∂θ=eθ,∂er∂ϕ=eϕsin⁡θ∂eθ∂θ=−er,∂eθ∂ϕ=eϕcos⁡θ∂eϕ∂θ=0,∂eϕ∂ϕ=−ersin⁡θ−eϕcos⁡θ\begin{cases}\frac{\partial\boldsymbol{e}_r}{\partial\theta}=\boldsymbol{e}_\theta ,\quad\frac{\partial\boldsymbol{e}_r}{\partial\boldsymbol{\phi}}=\boldsymbol{e}_\phi\sin\theta\\\\\frac{\partial\boldsymbol{e}_\theta}{\partial\theta}=-\boldsymbol{e}_r ,\quad\frac{\partial\boldsymbol{e}_\theta}{\partial\boldsymbol{\phi}}=\boldsymbol{e}_\phi\cos\theta\\\\\frac{\partial\boldsymbol{e}_\phi}{\partial\theta}=0 ,\quad\frac{\partial\boldsymbol{e}_\phi}{\partial\boldsymbol{\phi}}=-\boldsymbol{e}_r\sin\theta-\boldsymbol{e}_\phi\cos\theta\end{cases}

在球坐标系中，位置矢量为

r⃗=e⃗rr\vec{r}=\vec{e}_rr

其微分元矢量（线元矢量）为：

dl⃗=e⃗rdr+e⃗θrdθ+e⃗ϕrsin⁡θdϕ\mathrm{d}\vec{l}=\vec{e}_r\mathrm{d}r+\vec{e}_\theta r\mathrm{d}\theta+\vec{e}_\phi r\sin\theta\mathrm{d}\phi

度量系数分别为：

hr=1,hθ=r,hϕ=rsin⁡θh_{_r}=1 ,h_{_\theta}=r ,h_{_\phi}=r\sin\theta

在球坐标系中三个面积元分别为：

dS⃗r=e⃗rdlθdlϕ=e⃗rr2sinθdθdϕdS⃗θ=e⃗θdlrdlϕ=e⃗zrsinθdrdϕdS⃗ϕ=e⃗ϕdlrdlθ=e⃗ϕrdrdθ\begin{aligned} &\mathrm{d}\vec{S}_{r}=\vec{e}_{r}\mathrm{d}l_{\theta}\mathrm{d}l_{\phi}=\vec{e}_{r}r^{2}\mathrm{sin}\theta\mathrm{d}\theta\mathrm{d}\phi \\ &\mathrm{d}\vec{S}_\theta=\vec{e}_\theta\mathrm{d}l_r\mathrm{d}l_\phi=\vec{e}_zr\mathrm{sin}\theta\mathrm{d}r\mathrm{d}\phi \\ &\mathrm{d}\vec{S}_\phi=\vec{e}_\phi\mathrm{d}l_r\mathrm{d}l_\theta=\vec{e}_\phi r\mathrm{d}r\mathrm{d}\theta \end{aligned}

体积元为：

dV=r2sinθdrdθdϕ\mathrm{d}V=r^2\mathrm{sin}\theta\mathrm{d}r\mathrm{d}\theta\mathrm{d}\phi

1.3 标量场方向导数与梯度

若研究的物理量是一个标量，则该物理量所确定的场为标量场，可以用一个标量函数来表示，在直角坐标系中可表示为

u=u(x,y,z,t)u=u(x,y,z,t)

或用位置矢量表示为

u=u(r⃗,t)u=u(\vec{r},t)

如果与时间无关，可表示为

u=u(r⃗)u=u(\vec{r})

1.3.1 标量场的等值面

使标量函数u(r⃗)u(\vec{r})取得相同数值的点构成的空间曲面称为标量场的等值面，等值面方程为

u(r⃗)=cu(\vec{r})=c

标量场的等值面是互不相交的。

1.3.2 标量场的方向导数

设M0M_0为标量场u(M)u(M)中的一点，从点M0M_{0}出发引一条射线ll，点MM是射线ll上的动点，到点M0M_{0}的距离为Δl\Delta l。当点MM沿射线ll趋近于M0(M_0(即Δl→0)\Delta l\to0)时，比值u(M)−u(M0)Δl\frac{u(M)-u(M_0)}{\Delta l}的极限称为标量场 u(M)u(M)在点 M0M_{0}处沿ll方向的方向导数，记作∂u∂l∣M0\frac{\partial u}{\partial l}|{M_0}，即

∂u∂l∣M0=lim⁡Δl→0u(M)−u(M0)Δl\frac{\partial u}{\partial l}\Bigg|_{M_0}=\lim_{\Delta l\to0}\frac{u\left(M\right)-u\left(M_0\right)}{\Delta l}

当∂u∂l>0\frac{\partial u}{\partial l}>0 时，标量场 u(M)u(M)沿ll 方向是增加的；当∂u∂l<0\frac{\partial u}{\partial l}<0 时，标量场u(M)u(M)沿ll 方向是减小的；当∂u∂l=0\frac{\partial u}{\partial l}=0 时，标量场 u(M)u(M)沿 ll 方向无变化。

方向导数在直角坐标系中的计算公式

∂u∂l=∂u∂xdxdl+∂u∂ydydl+∂u∂zdzdl\frac{\partial u}{\partial l}=\frac{\partial u}{\partial x} \frac{\mathrm{d}x}{\mathrm{d}l}+\frac{\partial u}{\partial y} \frac{\mathrm{d}y}{\mathrm{d}l}+\frac{\partial u}{\partial z} \frac{\mathrm{d}z}{\mathrm{d}l}

若射线ll与xx、yy、zz轴的夹角分别为α\alpha、β\beta、γ\gamma,则有

dxdl=cos⁡α ,dydl=cos⁡β ,dzdl=cos⁡γ\frac{\mathrm{d}x}{\mathrm{d}l}=\cos\alpha\:,\frac{\mathrm{d}y}{\mathrm{d}l}=\cos\beta\:,\frac{\mathrm{d}z}{\mathrm{d}l}=\cos\gamma

式中 cosα\alpha、cosβ\beta、cosγ\gamma 为ll的方向余弦。于是，得到直角坐标系中方向导数的计算公式为

∂u∂l=∂u∂xcosα+∂u∂ycosβ+∂u∂zcosγ\frac{\partial u}{\partial l}=\frac{\partial u}{\partial x}\mathrm{cos}\alpha+\frac{\partial u}{\partial y}\mathrm{cos}\beta+\frac{\partial u}{\partial z}\mathrm{cos}\gamma

1.3.3 标量场的梯度

将标量场的梯度uu在点MM处的梯度定义为一个矢量，以符号grad ugrad\:u来表示，以en⃗\vec{e_n}表示变化率最大的方向的单位矢量，则

grad u=en⃗∂u∂l∣max\mathrm{grad}\: u=\vec{e_n}\left.\frac{\partial u}{\partial l}\right|_{\mathrm{max}}

grad ugrad\:u的方向即为标量场uu在点MM处变化率最大的方向，其模为即为最大变换率。

在直角坐标系中，梯度的计算公式为：

grad u=ex⃗(ex⃗⋅grad u)+ey⃗(ey⃗⋅grad u)+ez⃗(ez⃗⋅grad u)=ex⃗∂u∂x+ey⃗∂u∂y+ez⃗∂u∂z\begin{aligned}\mathrm{grad}\: u&=\vec{e_x}( \vec{e_x} \cdot \mathrm{grad}\: u )+\vec{e_y}( \vec{e_y} \cdot \mathrm{grad} \:u )+\vec{e_z}( \vec{e_z} \cdot \mathrm{grad}\: u )\\&=\vec{e_x} \frac{\partial u}{\partial x}+\vec{e_y} \frac{\partial u}{\partial y}+\vec{e_z} \frac{\partial u}{\partial z}\end{aligned}

在直角坐标系中，哈密顿算符“∇\nabla”(读作“del”或“Nabla”),

abla=ex⃗ ∂∂x+ey⃗ ∂∂y+ez⃗ ∂∂zabla=\vec{e_x}\:\frac{\partial}{\partial x}+\vec{e_y}\:\frac{\partial}{\partial y}+\vec{e_z}\:\frac{\partial}{\partial z}

算符 ∇\nabla具有矢量和微分的双重性质，故又称为矢性微分算符。因此，标量场uu 的梯度可用哈密顿算符 ∇\nabla表示为

grad u=( e⃗x ∂∂x+e⃗y ∂∂y+e⃗z ∂∂z) u= ∇u\mathrm{grad}\:u=\left(\:\vec{e}_x\:\frac{\partial}{\partial x}+\vec{e}_y\:\frac{\partial}{\partial y}+\vec{e}_z\:\frac{\partial}{\partial z}\right)\:u=\:\boldsymbol{\nabla}u

标量场uu的梯度可认为是算符∇\nabla作用于标量函数uu的一种运算。

在圆柱坐标系和球坐标系中，可以得到梯度的计算式分别为

ablau=eρ⃗∂u∂ρ+eϕ⃗∂uρ∂ϕ+ez⃗∂u∂z∇u=er⃗∂u∂r+eθ⃗∂ur∂θ+eϕ⃗∂ursinθ∂ϕabla u=\vec{e_\rho}\frac{\partial u}{\partial\rho}+\vec{e_\phi}\frac{\partial u}{\rho\partial\phi}+\vec{e_z}\frac{\partial u}{\partial z}\\ \nabla u=\vec{e_r}\frac{\partial u}{\partial r}+\vec{e_\theta}\frac{\partial u}{r\partial\theta}+\vec{e_\phi}\frac{\partial u}{r\mathrm{sin}\theta\partial\phi}

梯度运算遵循以下规则

abla(cu)=c∇u(c 为常数 )∇(u±v)=∇u±∇v∇(uv)=v∇u+u∇v∇(uv)=1v2(v∇u−u∇v)∇f(u)=f′(u)∇uabla(cu)=c\nabla u(c\text{ 为常数 })\\ \nabla\left(\begin{array}{c}u\pm v\end{array}\right)=\nabla u\pm\nabla v\\ \nabla\left(\begin{array}{c}uv\end{array}\right)=v \nabla u+u \nabla v\\ {\nabla}\bigg(\frac uv\bigg) =\frac1{v^2}( v{\nabla}u \boldsymbol{-}u {\nabla}v )\\ {\nabla}f( u )=f'( u ){\nabla}u

1.4 矢量场的通量和散度

若研究的物理量是一个矢量，该物理量确定的场称为矢量场，一个矢量场可用矢量函数来表示，在直角坐标系中可表示为

F⃗=F⃗(x,y,z,t)\vec{F}=\vec{F}(x,y,z,t)

或用位置矢量表示

F⃗=F⃗(r⃗,t)\vec{F}=\vec{F}(\vec{r},t)

若与时间无关，可表示为

F⃗=F⃗(r⃗)\vec{F}=\vec{F}(\vec{r})

在直角坐标系中

F⃗(x,y,z)=ex⃗Fx⃗(x,y,z)+ey⃗Fy⃗(x,y,z)+ez⃗Fz⃗(x,y,z)\vec{F}(x,y,z)=\vec{e_x}\vec{F_x}(x,y,z)+\vec{e_y}\vec{F_y}(x,y,z)+\vec{e_z}\vec{F_z}(x,y,z)

1.4.1 矢量场的矢量线

在直角坐标系中

dxFx=dyFy=dzFz\frac{\mathrm{d}x}{F_x}=\frac{\mathrm{d}y}{F_y}=\frac{\mathrm{d}z}{F_z}

1.4.2 矢量场的通量

设SS 为一空间曲面，dSdS为曲面SS上的面元，取一个与此面元相垂直的单位矢量 en⃗\vec{e_{n}}，则称矢量

dS⃗=e⃗ndS\mathrm{d}\vec{S}=\vec{e}_n\mathrm{d}S

为面元矢量。若为开曲面，则用右手螺旋法则确定en⃗\vec{e_n}的方向，若为闭曲面，则取外法线。

在矢量场F⃗\vec{F}中，任取一面元矢量 dS⃗d\vec{S}，矢量F⃗\vec{F}与面元矢量 dS⃗d\vec{S} 的标量积F⃗⋅dS⃗\vec{F}\cdot d\vec{S} 定义为矢量F⃗\vec{F}穿过面元矢量dS⃗d\vec{S}的通量。将曲面SS上各面元的F⃗⋅dS⃗\vec{F}\cdot d\vec{S}相加，则得到矢量F⃗\vec{F}穿过曲面 SS 的通量，即

Φ=∫SF⃗⋅dS⃗=∫SF⃗⋅en⃗dS\Phi = \int_{S}\vec{F} \cdot \mathrm{d}\vec{S} = \int_{S}\vec{F} \cdot \vec{e_{_n}}\mathrm{d}S

在直角坐标系中 ,dS=e⃗xd⁡Sx+e⃗yd⁡Sy+e⃗zd⁡SzdS=\vec e_x\operatorname{d}S_x+\vec e_y\operatorname{d}S_y+\vec{e}_z\operatorname{d}S_z，所以通量可以表示为

Φ=∫S( ex⃗Fx + ey⃗Fy + ez⃗Fz ) ⋅ ( ex⃗dSx + ey⃗dSy + ez⃗dSz )=∫S( Fx dSx + Fy dSy + FzdSz )\begin{aligned}\Phi&=\int_{S}(\:\vec{e_{x}}F_{x}\:+\:\vec{e_{y}}F_{y}\:+\:\vec{e_{z}}F_{z}\:)\:\cdot\:(\:\vec{e_{x}}\mathrm{d}S_{x}\:+\:\vec{e_{y}}\mathrm{d}S_{y}\:+\:\vec{e_{z}}\mathrm{d}S_{z}\:)\\&=\int_{S}(\:F_{x}\:\mathrm{d}S_{x}\:+\:F_{y}\:\mathrm{d}S_{y}\:+\:F_{z}\mathrm{d}S_{z}\:)\end{aligned}

若为闭合曲面，则通过闭合曲面的总通量可表示为

Φ=∮SF⋅dS=∮SF⋅endS\Phi =\oint_SF \cdot \mathrm{d}S =\oint_SF \cdot e_n\mathrm{d}S

当∮sF⃗⋅dS⃗>0\oint _s\vec F\cdot d\vec S> 0 时，称之为正通量源。当∮SF⃗⋅dS⃗<0\oint _{S}\vec F\cdot d\vec S< 0 时，称之为负通量源。例如，静电场中的负电荷就是汇聚电场线的负通量源；当∮sF⃗⋅dS⃗=0\oint{\mathrm{s}}\vec F \cdot d\vec S=0时，则闭合曲面SS内无通量源。

1.4.3 矢量场的散度

在矢量场FF中的任一点MM处作一个包围该点的任意闭合曲面SS，当曲面SS以任意方式收缩至点 MM 时 , 所限定的体积ΔV\Delta V将趋近于0,若比值∮sF⃗⋅dS⃗ΔV\frac{\oint_{s}\vec F\cdot\mathrm{d}\vec S}{\Delta V}的极限存在，则将此极限称为矢量场F⃗\vec F在点MM处的散度，并记作 div F⃗div \:\vec F,即

div F⃗ = lim⁡ΔV→0∮SF⃗ ⋅ dS⃗ΔV\mathrm{div}\:\vec F\:=\:\lim_{\Delta V\to0}\frac{\oint_{S}\vec F\:\cdot\:\mathrm{d}\vec S}{\Delta V}

div F⃗div\:\vec F描述的是通量源的密度，div F⃗div\:\vec F与体积元ΔV\Delta V的形状无关。

在直角坐标系中

div F⃗=lim⁡ΔV→0∮SF⃗⋅dS⃗ΔV=∂Fx∂x+∂Fy∂y+∂Fz∂z\mathrm{div}\: \vec{F} = \lim_{\Delta V\to0}\frac{\oint_S\vec{F} \cdot \mathrm{d}\vec{S}}{\Delta V} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}

利用算符∇\nabla ,可将 div Fdiv \:F表示为

div F⃗=( e⃗x ∂∂x+e⃗y ∂∂y+e⃗z ∂∂z) ⋅ ( e⃗xFx+e⃗yFy+e⃗zFz )= ∇ ⋅ F⃗\begin{aligned} \mathrm{div}\:\vec{F} &=\left(\:\vec{e}_{x}\:\frac{\partial}{\partial x}+\vec{e}_{y}\:\frac{\partial}{\partial y}+\vec{e}_{z}\:\frac{\partial}{\partial z}\right)\:\cdot\:(\:\vec{e}_{x}F_{x}+\vec{e}_{y}F_{y}+\vec{e}_{z}F_{z}\:)\\ &=\:\nabla\:\cdot\:\vec F \end{aligned}

类似地，可推出圆柱坐标系和球坐标系中的散度计算式，分别为

abla⋅F⃗=1ρ∂∂ρ(ρFρ)+1ρ∂Fϕ∂ϕ+∂Fz∂z∇⋅F⃗=1r2 ∂∂r( r2Fr )+1rsin⁡θ ∂∂θ( sin⁡θFθ )+1rsin⁡θ ∂Fϕ∂ϕabla\cdot \vec F=\frac1\rho\frac\partial{\partial\rho}(\rho F_\rho)+\frac1\rho\frac{\partial F_\phi}{\partial\phi}+\frac{\partial F_z}{\partial z}\\ \nabla\cdot \vec F=\frac{1}{r^2}\:\frac{\partial}{\partial r}(\:r^2F_r\:)+\frac{1}{r\sin\theta}\:\frac{\partial}{\partial\theta}(\:\sin\theta F_\theta\:)+\frac{1}{r\sin\theta}\:\frac{\partial F_\phi}{\partial\phi}

散度运算符合下列规则：

abla⋅(cF⃗)=c∇⋅F⃗(c为常数)∇⋅(F⃗±G⃗)=∇⋅F⃗±∇⋅G⃗∇⋅(uF⃗)=u∇⋅F⃗+F⃗⋅∇uabla\cdot(c\vec F)=c\nabla\cdot \vec F(c\text{为常数})\\ \nabla\cdot(\vec F\pm \vec G)=\nabla\cdot \vec F\pm\nabla\cdot \vec G\\ \nabla\cdot(u\vec F)=u\nabla\cdot \vec F+\vec F\cdot\nabla u

1.4.4 散度定理

散度定理（高斯定理）表述为

∫V∇⋅F⃗dV=∮SF⃗⋅dS⃗\int_V {\nabla}\cdot\vec{F}\mathrm{d}V=\oint_S\vec{F}\cdot \mathrm{d}\vec{S}

这个定理表明矢量场的散度在任意体积VV上的积分等于矢量场穿出限定该体积的闭合曲面SS的通量。

1.5 矢量场的环流与旋度

1.5.1 环流与环流面密度

矢量场F⃗\vec F沿场中的一条有向闭合路径CC的曲线积分

Γ=∮CF⃗⋅dl⃗\Gamma=\oint_C\vec F\cdot\mathrm{d}\vec l

称为矢量场F⃗\vec F沿闭合路径CC的环流，其中dl⃗d\vec l是路径上的线元矢量，其大小为 dldl、方向沿路径CC的切线方向，如图

矢量场F⃗\vec F中的点MM处选取一个方向e⃗n\vec e_n,并以e⃗n\vec e_n为法向量作一面元矢量ΔS⃗\Delta \vec S，其边界为有向闭合路径CC ,且CC的方向与面元ΔS⃗\Delta \vec S的法向矢量e⃗n\vec e_n成右螺旋关系，如图

当面元 ΔS⃗\Delta \vec S保持以e⃗n\vec e_n为法线方向以任意方式收缩至点MM 处时，若极限lim⁡ΔS→0∮cF⃗⋅dl⃗ΔS\lim_{\Delta S\to0}\frac{\oint_{c}\vec{F}\cdot\mathrm{d}\vec l}{\Delta S}存在，则称lim⁡ΔS→0∮cF⃗⋅dl⃗ΔS\lim_{\Delta S\to0}\frac{\oint_{c}\vec{F}\cdot\mathrm{d}\vec l}{\Delta S}为矢量场FF在点MM处沿方向e⃗n\vec{e}_n的环流面密度，并记作rot⁡nF⃗\operatorname{rot}_n\vec F,即

rot⁡nF⃗=lim⁡ΔS→0∮cF⃗⋅dl⃗ΔS\operatorname{rot}_n\vec{F} = \lim_{\Delta S\to0}\frac{\oint_c\vec{F}\cdot\mathrm{d}\vec{l}}{\Delta S}

环流面密度不仅与点MM的位置有关，还与面元矢量ΔS⃗\Delta \vec S的法向e⃗n\vec e_n有关。

1.5.2 矢量场的旋度

矢量场F⃗\vec F在点MM处的旋度定义为一个矢量，以符号rot F⃗rot\:\vec F(或 curl F⃗curl\:\vec F)来表示，它在点MM处沿方向e⃗n\vec e_n的分量等于矢量场F⃗\vec F在点MM处沿方向e⃗n\vec e_\mathrm{n}的环流面密度，即

en⋅ rot F⃗=rotnF⃗e_n\cdot\mathrm{~rot~}\vec F=\mathrm{rot}_n\vec F

所以当方向e⃗n\vec e_\mathrm{n}与rot F⃗rot \:\vec F的方向相同时，e⃗n⋅rot F⃗\vec e_\mathrm{n}\cdot rot \:\vec F的值最e⃗n⋅rot F⃗=∣rot F⃗∣\vec e_\mathrm{n}\cdot rot \:\vec F= | rot \:\vec F|。因此，rot F⃗rot\:\vec F的方向是使矢量场F⃗\vec F在点MM处取得最大环流面密度的方向，其模∣rot F⃗∣|rot \: \vec F|等于该最大环流面密度，即

rot F⃗=e⃗nm(lim⁡ΔS→01ΔS∮CF⃗⋅dl⃗)max\mathrm{rot~}\vec{F}=\vec{e}_{\mathrm{nm}}\left(\lim_{\Delta S\to0}\frac{1}{\Delta S}\oint_{C}\vec{F}\cdot\mathrm{d}\vec{l}\right)_{\mathrm{max}}

这里e⃗nm\vec e_\mathrm{nm}是矢量场F⃗\vec F在点MM处取得最大环流面密度的方向的单位矢量。

直角坐标系中，旋度的计算公式为

rot F⃗=e⃗x(∂Fz∂y−∂Fy∂z)+e⃗y(∂Fx∂z−∂Fz∂x)+e⃗z(∂Fy∂x−∂Fx∂y)\mathrm{rot} \:\vec{F} = \vec {e}_x\Bigg(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\Bigg) + \vec{e}_y\Bigg(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\Bigg) + \vec{e}_z\Bigg(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\Bigg)

利用算符∇\nabla ,可将 rot:F⃗rot:\vec F表示为

rot⁡F⃗=(e⃗x ∂∂x + e⃗y ∂∂y + e⃗z ∂∂z) × ( e⃗xFx + e⃗yFy + e⃗zFz)= ∇×F⃗\begin{aligned} \operatorname{rot}\vec{F}&=\left(\vec{e}_{x}\:\frac{\partial}{\partial x}\:+\:\vec{e}_{y}\:\frac{\partial}{\partial y}\:+\:\vec{e}_{z}\:\frac{\partial}{\partial z}\right)\:\times\:(\:\vec{e}_{x}F_{x}\:+\:\vec{e}_{y}F_{y}\:+\:\vec{e}_{z}F_{z})\\ &=\:\nabla\times \vec F\end{aligned}

上式亦可写成行列式形式

abla×F⃗=∣e⃗xe⃗ye⃗z∂∂x∂∂y∂∂zFxFyFz∣abla\times \vec F= \begin{vmatrix} \vec{e}_x&\vec{e}_y&\vec{e}_z\\\\\frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\\\F_x&F_y&F_z\end{vmatrix}

∇×F⃗\nabla\times \vec F在圆柱坐标系中的表达式为

abla×F⃗=e⃗ρ(1ρ∂Fz∂ϕ−∂Fϕ∂z) + e⃗ϕ(∂Fρ∂z−∂Fz∂ρ) +e⃗z1ρ[∂(ρFϕ)∂ρ−∂Fρ∂ϕ]abla\times \vec F=\vec e_\rho\left(\frac1\rho\frac{\partial F_z}{\partial\phi}-\frac{\partial F_\phi}{\partial z}\right)\:+\:\vec e_\phi\left(\frac{\partial F_\rho}{\partial z}-\frac{\partial F_z}{\partial\rho}\right)\:+\vec{e}_z\frac1\rho{\left[\frac{\partial\left(\rho F_\phi\right)}{\partial\rho}-\frac{\partial F_\rho}{\partial\phi}\right]}

写成行列式形式

abla×F⃗=1ρ∣e⃗ρρe⃗ϕe⃗z∂∂ρ∂∂ϕ∂∂zFρρFϕFz∣abla\times \vec F=\frac{1}{\rho}\left|\begin{array}{ccc}\vec{e}_\rho&\rho\vec{e}_\phi&\vec{e}_z\\\\ \frac{\partial}{\partial\rho}&\frac{\partial}{\partial\phi}&\frac{\partial}{\partial z}\\\\ F_\rho&\rho F_\phi&F_z\end{array}\right|

在球坐标系中，∇×F⃗\nabla\times \vec F的表达式为

∇×F⃗=e⃗r 1rsin⁡θ[ ∂∂θ( sin⁡θFϕ ) −∂Fθ∂ϕ] +e⃗θ 1r[ 1sin⁡θ ∂Fr∂ϕ−∂( rFϕ )∂r]+e⃗ϕ1r[∂(rFθ)∂r−∂Fr∂θ]{\nabla}\times\vec{F}=\vec{e}_r\:\frac{1}{r\sin\theta}\bigg[\:\frac{\partial}{\partial\theta}(\:\sin\theta F_\phi\:)\:-\frac{\partial F_\theta}{\partial\phi}\bigg]\:+\vec{e}_\theta\:\frac{1}{r}\bigg[\:\frac{1}{\sin\theta}\:\frac{\partial F_r}{\partial\phi}-\frac{\partial(\:rF_\phi\:)}{\partial r}\bigg]+\vec e_\phi\frac1r{\left[\frac{\partial(rF_\theta)}{\partial r}-\frac{\partial F_r}{\partial\theta}\right]}

写成行列式形式

abla×F⃗=1r2sin⁡θ∣e⃗rre⃗θrsin⁡θe⃗ϕ∂∂r∂∂θ∂∂ϕFrrFθrsin⁡θFϕ∣abla\times \vec F=\frac{1}{r^2\sin\theta}\left|\begin{array}{ccc}\vec e_r&r\vec{e}_\theta&r\sin\theta\vec{e}_\phi\\\\\frac{\partial}{\partial r}&\frac{\partial}{\partial\theta}&\frac{\partial}{\partial\phi}\\\\F_r&rF_\theta&r\sin\theta F_\phi\end{array}\right|

矢量场的旋度运算符合下列规则：

abla×(cF⃗)=c∇×F⃗(c为常数)∇×(F⃗±G⃗)=∇×F⃗±∇×G⃗∇×(uF⃗)=u∇×F⃗−F⃗×∇uabla \times (c\vec {F}) = c{\nabla }\times \vec{F}(c为常数 )\\ \nabla\times( \vec F\pm \vec G )=\nabla\times \vec F\pm \nabla\times \vec G\\ \nabla\times( u\vec F )=u \nabla\times \vec F-\vec F\times\nabla u

旋度和散度的比较：

  1. 旋度是矢量函数，散度是标量函数

  2. 散度描述的是标量源，即散度源；旋度描述的是矢量源，即漩涡源。散度源产生的矢量场的旋度处处为零，漩涡源产生的矢量场散度处处为零。

1.5.3 斯托克斯定理

斯托克斯定理（散度定理）：

∫S∇×F⃗⋅dS⃗=∮CF⃗⋅dl⃗\int_S \nabla\times \vec F\cdot\mathrm{d}\vec S=\oint_C\vec F\cdot\mathrm{d}\vec l

它表明矢量场F⃗\vec F的旋度∇×F⃗\nabla\times \vec F在曲面SS上的面积分等于矢量场F⃗\vec F在限定曲面的闭合曲线CC上的线积分，是矢量旋度的曲面积分与该矢量沿闭合曲线积分之间的一个变换关系，也是矢量分析中的一个重要的恒等式。

1.6 无旋场的标量位

如果一个矢量场F⃗\vec F的旋度处处为0，即

abla×F⃗≡0abla\times\vec F\equiv0

则称该矢量场为无旋场，它是由散度源所产生的。

任何标量场的梯度场一定是无旋场，即标量场的梯度的旋度恒等于0，即

abla×(∇u)≡0abla\times(\begin{array}{c}\nabla u\\\end{array})\equiv0

对于一个旋度处处为0的矢量场F⃗\vec F，总可以把它表示为某一标量场的梯度，即如果∇×F⃗≡0\nabla\times\vec F\equiv 0，存在标量函数，使得

F⃗=−∇u\vec F=-\nabla u

函数u称为无旋场F⃗\vec F的标量位函数，简称标量位。

1.7 无散场的矢量位

如果一个矢量场F⃗\vec F的散度处处为0，即

abla⋅F⃗≡0abla\cdot \vec F \equiv 0

则称该矢量场为无散场，它是由漩涡源所产生的。

任何矢量场的旋度场一定是无散场，即矢量场的旋度的散度恒等于0，即

abla⋅(∇×A⃗)=0abla\cdot( \nabla\times \vec A )=0

对于一个散度处处为 0 的矢量场 F⃗\vec F，总可以把它表示为某一矢量场的旋度，即如果 ∇⋅F⃗≡0\nabla\cdot \vec F\equiv0，则存在矢量函数 A⃗\vec A，使得

F⃗=∇×A⃗\vec F=\nabla\times \vec A

函数A⃗\vec A称为无散场F⃗\vec F的矢量位函数，简称矢量位。

1.8 格林定理

设uu 和vv是体积VV内具有连续二阶偏导数的两个任意标量函数，对矢量u∇vu\boldsymbol{\nabla}v应用散度定理，有

∫V ∇⋅ ( u ∇v ) dV=∮Su ∇v ⋅ e⃗n dS\int_V\:{\nabla}\cdot\:(\:u\:{\nabla}v\:)\:\mathrm{d}V=\oint_Su\:{\nabla}v\:\cdot\:\vec{e}_\mathrm{n}\:\mathrm{d}S

式中，SS是体积VV的边界面，e⃗n\vec e_{\mathrm{n}}为曲面SS的外法向单位矢量。由于

abla ⋅ ( u ∇v )=u ∇2v+ ∇u ⋅ ∇vabla\:\cdot\:(\:u\:\nabla v\:)=u\:\nabla^2v+\:\nabla u\:\cdot\:\nabla v

代入上式得到

∫V(u∇2v+∇u⋅∇v) dV=∮Su ∇v ⋅ e⃗ndS\int_V(\begin{array}{cccc}u&\nabla^2v&+&\nabla u&\cdot&\nabla v\end{array})\:\mathrm{d}V=\oint_Su\:\nabla v\:\cdot\:\vec{e}_n\mathrm{d}S

此式称为格林第一恒等式。

格林第二恒等式可写成

∫V(u∇2v−v∇2u)dV=∮S(u∇v−v∇u)⋅e⃗ndS\int_V( u {\nabla}^2v - v {\nabla}^2u ) \mathrm{d}V=\oint_S( u {\nabla}v - v {\nabla}u ) \cdot \vec{e}_n\mathrm{d}S

或

∫V(u∇2v−v∇2u)dV=∮S(u∂v∂n−v∂u∂n)dS\int_V( u \nabla^2v - v \nabla^2u ) \mathrm{d}V=\oint_S\biggl( u \frac{\partial v}{\partial n} - v \frac{\partial u}{\partial n}\biggr) \mathrm{d}S

1.9 亥姆霍兹定理

亥姆霍兹定理表述为在有限的区域VV内，任一矢量场由它的散度、旋度和边界条件(即限定区域VV的闭合面SS上的矢量场的分布)唯一地确定，且可表示为

F⃗(r⃗)=−∇u(r⃗)+∇×A⃗(r⃗)\vec{F}\left(\vec{r}\right)=-{\nabla}u\left(\vec{r}\right)+{\nabla}\times\vec{A}\left(\vec{r}\right)

其中

u(r⃗)=14π∫V∇′⋅F⃗(r⃗′)∣r⃗−r⃗′∣dV′−14π∮Se⃗n′⋅F⃗(r⃗′)∣r⃗−r⃗′∣dS′A⃗(r⃗)=14π∫V∇′×F⃗(r⃗′)∣r⃗−r⃗′∣dV′−14π∮Se⃗n′×F⃗(r⃗′)∣r⃗−r⃗′∣dS′u\left(\vec{r}\right)=\frac{1}{4\pi}\int_{V}\frac{{\nabla}^{\prime}\cdot\vec{F}(\vec{r}^{\prime})}{\mid\vec{r}-\vec{r}^{\prime}\mid}\mathrm{d}V^{\prime}-\frac{1}{4\pi}\oint_{S}\frac{\vec{e}^{\prime}_{n}\cdot\vec{F}(\vec{r}^{\prime})}{\mid\vec{r}-\vec{r}^{\prime}\mid}\mathrm{d}S^{\prime}\\ \vec A\left(\vec r\right)=\frac{1}{4\pi}\int_{V}\frac{\nabla'\times \vec F\left(\vec r'\right)}{\left|\vec r-\vec r'\right|}\mathrm{d}V'-\frac{1}{4\pi}\oint_{S}\frac{\vec e'_{n}\times \vec F\left(\vec r'\right)}{\left|\vec r-\vec r'\right|}\mathrm{d}S'

它表明

  1. 矢量场F⃗\vec F可以用一个标量函数的梯度和一个矢量函数的旋度之和来表示。此标量函数由F⃗\vec F的散度和F⃗\vec F在边界SS上的法向分量完全确定；而矢量函数则由F⃗\vec F的旋度和F⃗\vec F在边界面SS上的切向分量完全确定。

  2. 由于∇×[∇u(r⃗)]≡0,∇⋅[∇×A(r⃗)]≡0\nabla \times [\nabla u( \vec{r})] \equiv 0, \nabla \cdot [\nabla \times A( \vec{r})] \equiv 0，因而一个矢量场可以表示为一个无旋场与无散场之和，即

    F⃗=F⃗l+F⃗C\vec F=\vec F_{l}+\vec F_{C}

    其中

    {∇⋅Fl=∇⋅F∇×Fl=0,{∇⋅FC=0∇×FC=∇×F\left.\left\{\begin{array}{ll}\nabla \cdot F_{_l}= \nabla \cdot F\\\\\nabla\times F_{_l}=0 ,\end{array}\right.\right.\left\{\begin{array}{ll}\nabla \cdot F_{_C}=0\\ \\\nabla\times F_{_C}= \nabla\times F\end{array}\right.

  3. 如果在区域VV内矢量场 F⃗\vec F 的散度与旋度均处处为 0,则 F⃗\vec F 由其在边界面 SS上的场分布完全确定；

  4. 对于无界空间，只要矢量场满足

    ∣F⃗∣∝1/∣r⃗−r⃗′∣1+δ(δ>0)\mid \vec F\mid\propto1/\mid \vec r-\vec r^{\prime}\mid^{1+\delta}\quad(\delta>0)

    此时，矢量场由其散度和旋度完全确定。因此，在无界空间中，散度与旋度均处处为 0 的矢量场是不存在的，因为任何一个物理场都必须有源，场是同源一起出现的，源是产生场的起因。

亥姆霍兹定理总结了矢量场的基本性质，其意义是非常重要的。分析矢量场时，总是从研究它的散度和旋度着手，得到的散度方程和旋度方程组成了矢量场的基本方程的微分形式；或者从矢量场沿闭合曲面的通量和沿闭合路径的环流着手，得到矢量场的基本方程的积分形式。

Previous电磁场与电磁波Next信息安全技术

Last updated