🧆4. 信道

按传输媒介，信道可分为：

1. 有线信道

2. 无线信道

按信道特性，信道可分为：

1. 恒定参量信道

2. 随机参量信道

4.1 无线信道

地球大气层的结构：

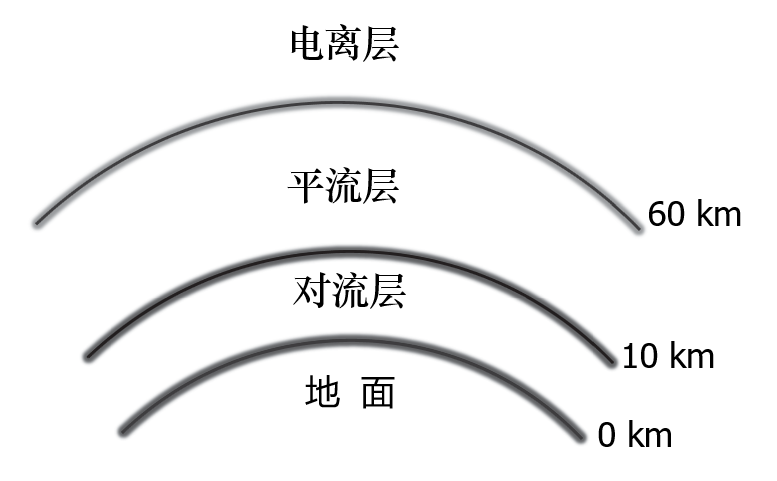
电磁波的传播方式：

1. 地波（ground-wave）：频率小于2MHz，有绕射能力，传播距离数百或数千米，常用于AM广播

   
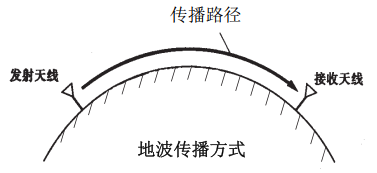
2. 天波（sky-wave）：频率介于2~30MHz，被电离层反射，传播距离（一跳）小于4000km，多跳可达10000km，常用于远程、短波通信

   
3. 视距传播（Line-of-Sight(LOS)）：频率大于30MHz（高频），直线传播，可穿透电离层，常用于卫星和外太空通信，超短波及微波通信，传播距离与天线高度有关

   

   $$h=\frac{D^{2}}{8r}\approx\frac{D^{2}}{50}(m)$$

   可以通过提升天线高度，通过微波中继（微波接力），卫星中继（静止卫星、移动卫星），平流层通信（充氦飞艇、气球、飞机代替卫星）来增大视距传播距离的途径。

   1. 微波中继

      

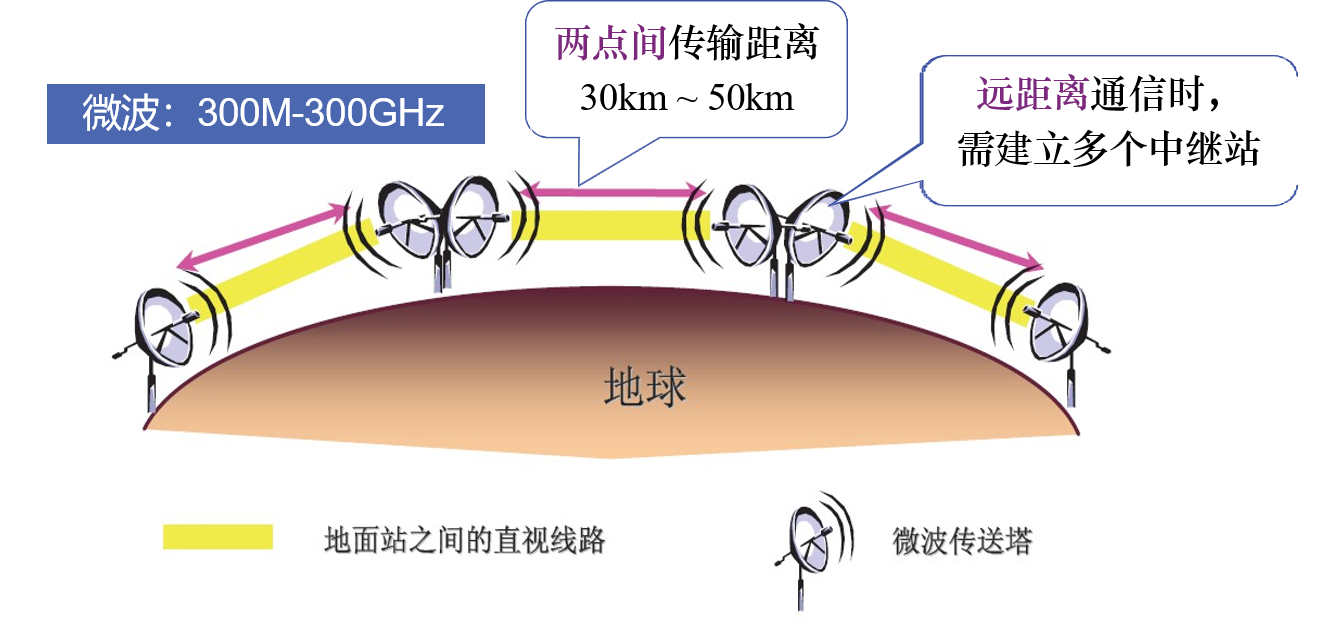
      • 优点：容量大、投资少、维护方便、传输质量稳定

      • 应用：远距离传输话音和电视信号

   2. 卫星中继

      • 优点：信道容量大、传输质量稳定、传输距离远、覆盖区域广

      • 缺点：传输时延大、信号衰减大、造价高

      • 应用：航空通信、GPS

4. 散射通信

   1. 电离层散射

      • 机理：由电离层不均匀性引起

      • 频率：30~60MHz

      • 距离：>1000km

   2. 对流层散射

      • 机理：由对流层不均匀性（湍流）引起

      • 频率：100~4000MHz

      • 距离：<600km

   3. 流星余迹散射

      • 特性：高度80~120km，长度15~40km，存留时间：小于1秒至几分钟

      • 频率：30~100MHz

      • 距离：1000km以上

      • 用途：低速存储、高速突发、断续传输

多径传播：信号经过不同的传播路径，形成了多个反射副本，副本信号经过不同的幅度衰落和相位变化最终到达接收机，在接收机形成叠加效应，如图

$$r(t)=\sum_{n=0}^{N-1}A_ne^{j\phi_n}x(t-T_n)$$

终端在环境中移动时，多径反射信号的幅度/相位将发生改变

4.2 有线信道

1. 明线

   • 传输损耗低

   • 易受天气影响

   • 布线复杂

2. 对称电缆

   

   • 特点：每对呈纽绞状，以减少各线对的相互干扰

   • 缺点：传输衰减大/距离短，邻道间有串话干扰

   • 应用：电话线路、局域网及综合布线工程中的传输介质

   • 分类：

     • 非屏蔽双绞线（UTP）：便宜、易弯曲、易安装

     • 屏蔽双绞线（STP）：每对加有接地的金属箔屏蔽层，可减少噪声干扰

3. 同轴电缆

   

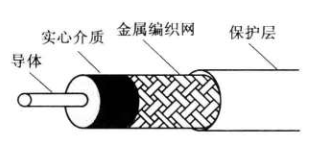
   • 组成：由两个导体组成，内芯为金属导线，外导体为金属编织网

   • 优点：抗电磁干扰能力强，带宽更高、速率更高

   • 缺点：成本较高

   • 分类：

     • 基带同轴电缆：50$\Omega$，多用于数字基带传输，速率可达10Mb/s，传输距离<几千米

     • 宽带（射频）同轴电缆：75$\Omega$，用于传输模拟信号，多用于有线电视（CATV）系统，传输距离可达几十千米

4. 光纤

   • 光导纤维：由光波承载信息，通常由玻璃或塑料纤维制成

   • 结构：纤芯和包层构成的双层通信圆柱体

   • 按折射率分类：阶跃型和梯度型

   • 按模式（光线传播路径）分类：多模光纤和单模光纤

   • 优点：

     • 传输带宽、信道容量大：远大于金属电缆（双绞线和同轴电缆）

     • 传输衰减少，无中继传输距离远

     • 抗电磁干扰，传输质量好，防窃听（军事通信和商业保密），耐腐蚀（远程海底通信）

     • 体积小，重量轻，节省有色金属，环保

   • 缺点：

     • 易碎，接口昂贵，安装和维护的技术门槛高

   • 应用：长途电话网、有线电视网、蜂窝网络等主干网络

4.3 信道的数学模型

信道有调制信道和编码信道两种定义，如图

4.3.1 调制信道模型

模型：叠加有噪声的线性时变/时不变网络：

共性：

• 有一对（或多对）输入端和输出端

• 大多数信道都满足线性叠加原理

• 对信号有固定或时变的延迟和损耗

• 无信号输入时，仍可能有输出（噪声）

入出关系：

$$r(t)=s_o(t)+n(t)$$

其中

$$s_{{o}}(t)=f[s_i(t)]=c(t)*s_i(t)$$

所以

$$S_{_0}(\omega)=C(\omega)S_{_i}(\omega)$$

调制信道对信号的影响程度取决于$C(\omega)$和$n(t)$的特性，信道特性是一个复杂的函数，它可能会使信号产生包括各种线性或非线性的失真、延时和衰落。

调制信道根据信道的时变特性，可分为恒参信道（特性基本不随环境发生变化），随参信道（特性随时间随机快变化）。

若$C(\omega)$常数（通常为1），则信道模型为加性高斯白噪声模型。

4.3.2 编码信道模型

模型：是一种数字信道或离散信道，输入输出均为离散信号，输入数字序列得到另一输出数字序列，因信道噪声等因素的影响，输出数字序列将可能发生错误，输入、输出数字序列之间的关系可用一组转移概率表征。

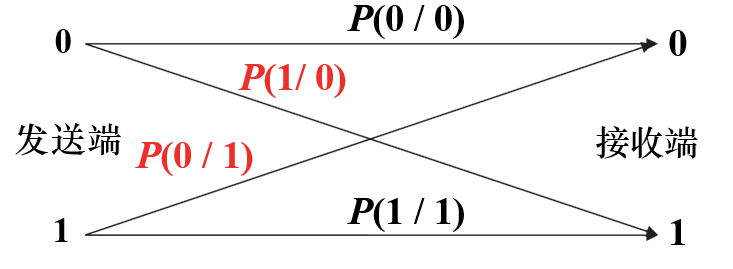
其中

$$P(0/0)+P(1/0)=1\\ p(1/1)+P(0/1)=1$$

误码率

$$P_e=P(0)P(1/0)+P(1)P(0/1)$$

4.4 信道特性及其对信号传输的影响

4.4.1 恒参信道

恒参信道举例：

• 各种有线信道

• 卫星信道

恒参信道其实是一个线性时不变系统，其传输特性为

$$H(\omega)=\left|H(\omega)\right|e^{j\phi(\omega)}$$

其中$|H(\omega)|\sim\omega$描述的是幅频特性，$\phi(\omega)\sim\omega$描述的是相频特性。

若为无失真传输，传输特性可写成

$$H(\omega)=Ke^{-j\omega t_d}$$

其中$|H(\omega)|=K$，$\phi(\omega)=\omega t_d$，群时延特性为$\tau(\omega)=\frac{d\varphi(\omega)}{d\omega}=t_d$。

无失真传输特性曲线如下图

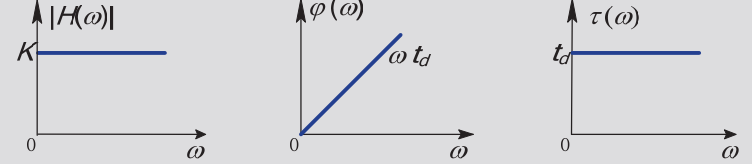
理想恒参信道的冲激响应：

$$h(t)=K\delta(t-t_d)$$

若输入信号为$s(t)$，则理想恒参信道的输出为

$$s_{\mathrm{o}}(t)=Ks(t-t_{d})$$

这种情况称为无失真传输。

但在实际的传输过程中，会产生失真，带来的影响如下：

• 幅频失真：$\left|H(\omega)\right|\neq K$，影响：

  • 对模拟信号：造成波形失真$\to$信噪比下降

  • 对数字信号：产生码间串扰$\to$误码率增大

• 相频失真：$\phi(\omega)\neq\omega t_d$，影响：

  • 对语音信号影响不大，对视频信号影响大

  • 对数字信号：码间串扰$\to$误码率增大

4.4.2 随参信道

随参信道举例：

• 陆地移动信道

• 短波电离层反射信道

• 超短波流星余迹散射信道

• 超短波及微波对流层散射信道

• 超短波电离层散射

• 超短波超视距绕射

随参信道特性：

• 衰减随时间变化

• 时延随时间变化

• 多径传播

现在来探究多径传播产生的多径效应对信号的影响，设发射信号为幅度恒定，频率单一的信号，即$s(t)=A\cos\omega_ct$，若该信号经过$n$条路径传播，且各路径有时变的衰落和传输延迟，信号经过各路径到达接收端的信号相互独立，则接收信号为

$$\begin{aligned} r(t)& =a_1(t)\cos\omega_c\left[t-\tau_1(t)\right]+a_2(t)\cos\omega_c\left[t-\tau_2(t)\right] +\cdots+a_n(t)\cos\omega_c\begin{bmatrix}t-\tau_n(t)\end{bmatrix} \\ &=\sum_{i=1}^na_i(t)\cos\omega_c\begin{bmatrix}t-\tau_i(t)\end{bmatrix} \\ &=\sum_{i=1}^na_i(t)\cos[\omega_ct+\varphi_i(t)] \end{aligned}$$

其中，$\varphi_i(t)=-\omega_c\tau_i(t)$

将上式继续展开，有

$$\begin{aligned} r(t)& =\sum_{i=1}^na_i(t)\cos\varphi_i\cos\omega_ct-\sum_{i=1}^na_i(t)\sin\varphi_i\sin\omega_ct \\ &=X(t)\cos\omega_ct-Y(t)\sin\omega_ct \\ &=V(t)\cos\left[\omega_ct+\varphi(t)\right] \end{aligned}$$

其中，$V(t)$服从瑞利分布，$\varphi(t)$服从均匀分布，$X(t)=\sum_{i=1}^na_i(t)\cos\varphi_i$，$Y(t)=\sum_{i=1}^na_i(t)\sin\varphi_i$，根据概率论的中心极限定理，当路径数量n足够大时，$X(t)$和$Y(t)$趋于正态分布。

由上可知，接收信号是包络、相位随机缓变的窄带信号，其波形和频谱如下

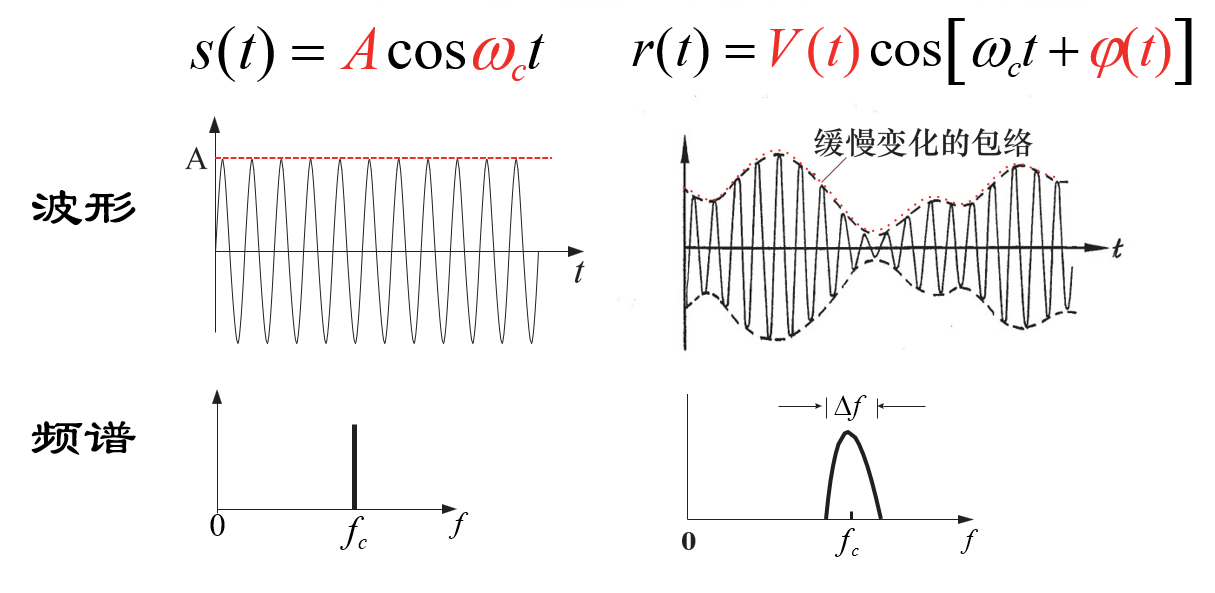
因此多径传播会使信号产生瑞利衰落，同时会引起频率弥散。

对于一个复杂信号$f(t)$，探讨多径传播对其影响。从两条路径推广到多条路径，设两条路径的信道的传输衰减均为$K$，传输时延分别为$\tau_1$和$\tau_2$，接收信号为

$$\begin{aligned}f_0(t)&=Kf(t-\tau_1)+Kf(t-\tau_2)\\F_0(\omega)&=KF(\omega)e^{-j\omega\tau_1}+KF(\omega)e^{-j\omega(\tau_1+\tau)}\end{aligned}$$

式中$\tau=\tau_2-\tau_1$表示相对时延差，则信道传输函数为

$$H(\omega)=\frac{F_\mathrm{o}(\omega)}{F(\omega)}=Ke^{-j\omega\tau_1}(1+e^{-j\omega\tau})$$

忽略常数$K$，则信道幅频特性为

$$\left|H(\omega)\right|=\left|1+e^{-j\omega\tau}\right|=2\left|\cos\frac{\omega\tau}2\right|$$

如图

所以信道对信号不同的频率成分，将有不同程度的时变衰减，这称为频率选择性衰落。

多径信道的相干带宽：

$$\Delta f=1/\tau_{\mathrm{m}}$$

定义为相邻传输零点的频率间隔，为了减少频率选择性衰落的影响，我们应该使信号带宽$B_s<\Delta f$，工程经验公式：

$$B_s=(1/3\thicksim1/5)\triangle f$$

数字信号的码元宽度：

$$T_s=(3\thicksim5)\tau_m$$

同时我们还可以采取分集接收、扩频技术、OFDM等高级技术。

4.5 信道噪声

信道中存在的不需要的电信号统称为噪声，它独立于信号始终存在，又称加性干扰，它使信号失真，发生误码，降低传输速率。

噪声类型：

1. 按噪声来源：

   1. 人为噪声

   2. 自然噪声（各种电磁波）

   3. 内部噪声（热噪声）

2. 按噪声性质：

   1. 脉冲噪声（电火花）

   2. 窄带/单频噪声（电子设备）

   3. 起伏噪声（热噪声、散弹噪声和宇宙噪声）

热噪声：

• 来源于一切电阻性元器件中电子的（布朗）热运动

• 均匀分布在$0\thicksim10^{12}$频率范围

• 性质：高斯白噪声

• 电压的有效值：

  $$V=\sqrt{4kTRB}\quad\text{(V)}$$

  式中：

  • $k=1.38\times10^{-23}$ $k=1.38\times10^{-23}(J/K)$ 一波兹曼常数

  • $T-$热力学温度 ($\degree K$)

  • $R-$阻抗 $(\Omega)$

  • $B-$带宽(Hz)

信道加性白噪声$n(t)$:

• 代表：起伏噪声（热噪声等）

• 性质：高斯白噪声

• 功率谱密度：

  $$P_n(f)=\frac{n_0}2(\mathrm{W/Hz})$$
• 自相关函数：

  $$R_n(\tau)=\frac{n_0}2\delta(\tau)$$
• 概率密度函数：

  $$f_n(\nu)=\frac1{\sqrt{2\pi}\sigma_n}\exp\biggl(-\frac{\nu^2}{2\sigma_n^2}\biggr)$$
• $n(t)$通过BPF（带通滤波器）会变成窄带高斯噪声。

设窄带高斯噪声的双边功率谱密度为$P_n(f)$，如图

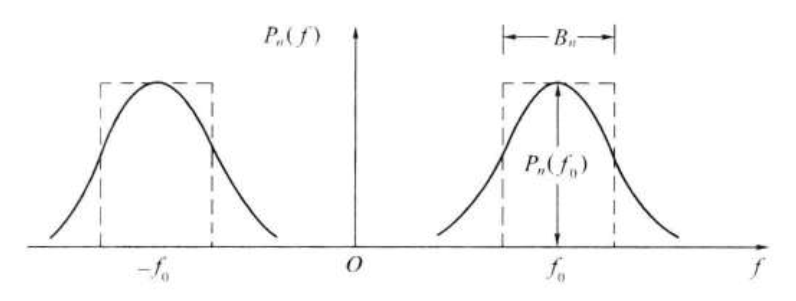
此噪声的功率为：

$$N = \int_{-\infty}^{\infty}P_{n}( f )df$$

为了描述窄带噪声的带宽，引入噪声等效带宽的概念，即将功率谱密度形状变为矩形，并保持噪声功率不变，则矩形宽度为：

$$B_n=\frac{\int_{-\infty}^\infty P_n(f)df}{2P_n(f_0)}=\frac{\int_0^\infty P_n(f)df}{P_n(f_0)}$$

物理意义：通过宽度为$B_n$的矩形滤波器的噪声功率=通过实际接收滤波器的噪声功率

4.6 信道容量

信道容量：指信道能够无差错传输时的最大平均信息速率

4.6.1 离散信道容量

信道模型如图

图中发送符号$x_1,x_2,...,x_n$出现的概率为；收到$y_j$的概率是$P(y_j)$，$j=1,2,...,m$。$P(y_j/x_i)$是转移条件概率，即发送$x_i$的条件下收到$y_j$的概率

1. 信源发送的平均信息量（熵）

   $$H(x)=-\sum_{i=1}^{n}P(x_{i})\log_{2}P(x_{i})$$

   式中，$P(x_i)$为发送符号$x_i$的概率($i=1,2,3,...,n$)

2. 接收端的平均信息量

   接收端收到$y_j$后对$x_i$的不确定度为

   $$H(x/y)=-\sum_{j=1}^mP(y_j)\sum_{i=1}^nP(x_i/y_j)\log_2P(x_i/y_j)$$

   式中，$P(y_j)$为收到$y_j$的概率，$P(x_i/y_j)$为收到$y_j$后判断发送的是$x_i$的转移概率。

   所以接收端的平均信息量为

   $$平均信息量/符号=H(x)-H(x/y)$$
3. 信息传输速率$R$——信道每秒传输的平均信息量

   $$R=r[H(x)-H(x/y)]\quad\mathrm{(b/s)}$$

   式中，$r$为信道每秒传输的符号数

4. 信道容量

   即为最大信息传输速率：对一切可能的信源概率分布，求$R$的最大值：

   $$C_{\mathfrak{t}}=\max_{P(x)}\{R\}=\max_{P(x)}\{r[H(x)-H(x/y)]\} (\mathrm{b/s})$$

   等价于

   $$C=\max_{P(x)}[H(x)-H(x/y)](b/\text{符号})$$

   所以信道容量有两种度量单位：

   1. 用每个符号能够传输的平均信息量的最大值来表示信道容量

   2. 用单位时间内能够传输的平均信息量的最大值来表示信道容量

4.6.2 连续信道容量

由香农信息论可证，白噪声背景下的连续信道容量为：

$$C=B\log_2\left(1+\frac{S}{N}\right)\text{ (b/s)}$$

也可写为

$$C=B\operatorname{log}_{2}\Bigg(1+\frac{S}{n_{0}B}\Bigg) \mathrm{(b/s)}$$

式中，$S$——信号平均功率($W$)；$B$——带宽($Hz$)；$n_0$——噪声单边带功率谱密度；$N=n_0B$——噪声功率($W$)

含义：当信号和信道噪声的平均功率给定时，在具有一定频带宽度的信道上，理论上单位时间内可能传输的信息量的极限数值。

意义： 若$R_b\boldsymbol{<}=C$ ，则总能找到一种信道编码方式，实现无差错传输；若传输速率大于信道容量，则不可能实现无差错传输。

香农公式给出了通信系统所能达到的极限信息传输速率，但是只证明了理想通信系统的“存在性”，却未指出其实现方法。

结论：

• 信道容量$C$依赖于$B$、$S$ 和$n_0$

• 增大$S$可增加 $C$，若$\mathcal{S}\to\infty$，则$C\to\infty;$

• 减小 $n_0$ 可增加 $C$，若$n_0\to0$，则$C\to\infty;$

• 增大$B$可增加$C$，但不能使$C$无限制增大当$B\to\infty$时，${C}$将趋向一个由信噪比决定的定值：

通过计算，可知：

$$\lim_{B\to\infty}C=\lim_{B\to\infty}B\log_2(1+\frac S{n_0B})\approx1.44\frac S{n_0}$$