3. 随机过程

3.1 随机过程的基本概念

随机过程可以从两个不同的角度来说明。

把随机过程看成对应不同随机试验结果的时间过程的集合。
把随机过程看作是在时间进程中处于不同时刻的随机变量的集合。

3.1.1 随机过程的分布函数

设 $\xi(t)$ 表示一个随机过程，则它在任意时刻 $t_1$ 的值 $\xi(t_1)$ 是一个随机变量，其一维分布函数( distribution function)为

F_{_1}(\:x_{_1}\:,t_{_1}\:)\:=\:P[\:\xi(\:t_{_1}\:)\:\leqslant\:x_{_1}\:]

一维概率密度( probability density) 函数为

\frac{\partial F_1(\:x_1\:,t_1\:)}{\partial x_1}\:=f_1(\:x_1\:,t_1\:)

一维分布函数或一维概率密度函数仅仅描述了随机过程在任一瞬间的统计特性，它对随机过程的描述很不充分。进而对于任意固定的 $t_1$ 和 $t_2$ 时刻，随机过程 $\xi(t)$ 的二维分布函数为

F_2(\:x_1\:,x_2\:;t_1\:,t_2\:)\:=\:P\{\:\xi(\:t_1\:)\:\leqslant\:x_1\:,\xi(\:t_2\:)\:\leqslant\:x_2\}

$\xi(t)$ 的二维概率密度函数为

\frac{\partial^2F_2(\:x_1\:,x_2\:;t_1\:,t_2\:)}{\partial x_1\:\cdot\:\partial x_2}\:=f_2(\:x_1\:,x_2\:;t_1\:,t_2\:)

任意给定 $t_1,t_2,\cdots,t_n\in T$ ,则 $\xi(t)$ 的 $n$ 维分布函数定义为

F_n(\begin{array}{c}x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n\end{array})\\ =P\{\xi(\:t_1\:)\:\leqslant\:x_1\:,\xi(\:t_2\:)\:\leqslant\:x_2\:,\cdots,\xi(\:t_n\:)\:\leqslant\:x_n\:\}

$\xi(t)$ 的 n 维概率密度函数为

\frac{\partial^nF_n(\:x_1\:,x_2\:,\cdots,x_n\:;t_1\:,t_2\:,\cdots,t_n\:)}{\partial x_1\:\partial x_2\:\cdots\:\partial x_n}=f_n(\:x_1\:,x_2\:,\cdots,x_n\:;t_1\:,t_2\:,\cdots,t_n\:)

$n$ 越大，对随机过程统计特性的描述就越充分。

3.1.2 随机过程的数字特征

均值（数学期望）
定义：
$E[\:\xi(\:t\:)\:]\:=\:\int_{-\infty}^{\infty}xf_{1}(\:x\:,t\:)\:\mathrm{d}x$
$\xi(t)$ 的均值 $E[\xi(t)]$ 是时间的确定函数，常记为 $a(t)$ ，它表示随机过程的 $n$ 个样本函数曲线的摆动中心。
方差
定义：
$D[\:\xi(\:t)\:]\:=\:E\{\:[\:\xi(\:t)\:-\:a(\:t)\:]^{2}\:\}$
$D[\xi(t)]$ 常记为 $\sigma^2(t)$ 。
由
$\begin{aligned}D[ \xi(t) ]&= E[ \xi^{2}( t ) - 2a( t )\xi( t ) + a^{2}( t ) ] = E[ \xi^{2}( t ) ] - 2a( t ) E[ \xi( t ) ] + a^{2}( t )\\&= E[ \xi^{2}\left( t \right) ] - a^{2}\left( t \right) = \int_{-\infty}^{\infty}x^{2}f_{1}\left( x ,t \right)\mathrm{d}x - \left[ a\left( t \right) \right]^{2}\end{aligned}$
可知方差等于均方值与均值平方之差，它表示随机过程在时刻 $t$ 相对于均值 $a(t)$ 的偏离程度。
相关函数
随机过程 $\xi(t)$ 的协方差函数定义为
$\begin{align*} B(t_{1},t_{2})&=E\{\left[\xi(t_{1})-a(t_{1})\right]\left[\xi(t_{2})-a(t_{2})\right]\}\\ &=\:\int_{-\infty}^{\infty}\:\int_{-\infty}^{\infty}\left[\:x_{1}\:-\:a(\:t_{1}\:)\:\right]\left[\:x_{2}\:-\:a(\:t_{2}\:)\:\right]f_{2}(\:x_{1}\:,x_{2}\:;t_{1}\:,t_{2}\:)\:\mathrm{d}x_{1}\:\mathrm{d}x_2 \end{align*}$
式中 $:a(t_1)$ 和 $a(t_2)$ 分别是在 $t_1$ 和 $t_2$ 时刻得到的 $\xi(t)$ 的均值； $f_2(x_1,x_2;t_1,t_2)$ 为 $\xi(t)$ 的二维概率密度函数。
随机过程 $\xi(t)$ 的自相关函数定义为
$R(\:t_1\:,t_2\:)\:=\:E[\:\xi(\:t_1\:)\xi(\:t_2\:)\:]\:=\:\int_{-\infty}^{\infty}\:\int_{-\infty}^{\infty}\:x_1x_2f_2(\:x_1\:,x_2\:;t_1\:,t_2\:)\:\mathrm{d}x_1\:\mathrm{d}x_2$
式中 $:\xi(t_1)$ 和 $\xi(t_2)$ 分别是在 $t_1$ 和 $t_2$ 时刻观测 $\xi(t)$ 得到的随机变量。
$R(t_1,t_2)$ 与 $B(t_1,t_2)$ 之间有着如下确定的关系：
$B(\:t_1\:,t_2\:)\:=\:R(\:t_1\:,t_2\:)\:-\:a(\:t_1\:)\:a(\:t_2\:)$
若随机过程的均值为0，则 $B(t_1,t_2)$ 与 $R(t_1,t_2)$ 完全相同。
如果把相关函数的概念引伸到两个或更多个随机过程，可以得到互相关函数。设 $\xi(t)$ 和 $\eta(t)$ 分别表示两个随机过程，则互相关函数定义为
$R_{\xi\eta}(\:t_1\:,t_2\:)\:=\:E[\:\xi(\:t_1\:)\:\eta(\:t_2\:)\:]$

3.2 平稳随机过程

3.2.1 定义

若一个随机过程 $\xi(t)$ 的统计特性与时间起点无关，即时间平移不影响其任何统计特性，则称该随机过程是在严格意义下的平稳随机过程，简称严平稳随机过程。

它的一维概率密度函数与时间 $\tau$ 无关，即

f_1\left(x_1,t_1\right)=f_1\left(x_1\right)

而二维分布函数只与时间间隔 $\tau=t_2-t_1$ 有关，即

f_2(\:x_1\:,x_2\:;t_1\:,t_2\:)\:=f_2(\:x_1\:,x_2\:;\tau\:)

其均值和自相关函数分别为

E[\:\xi(\:t)\:]\:=\:a\\ R(\:t_{1}\:,t_{2}\:)=R(\:\tau\:)

实际中我们常用这均值和自相关函数这两个条件来直接判断随机过程的平稳性，并把同时满足上式的过程定义为广义平稳( generalized stationary)随机过程。显然，严平稳随机过程必定是广义平稳的，反之不一定成立。

3.2.2 各态历经性

平稳过程 $\xi(t)$ 的时间均值和时间相关函数分别定义为

\begin{cases} &\overline{a}\:=\:\overline{x(\:t\:)}\:=\:\lim_{T\to\infty}\frac{1}{T}\int_{-T/2}^{T/2}x(\:t\:)\:\mathrm{d}t\\ \\&\overline{R(\:\tau\:)}\:=\:\overline{x(\:t\:)\:x(\:t\:+\:\tau\:)}\:=\:\lim_{T\to\infty}\:\frac{1}{T}\int_{-T/2}^{T/2}x(\:t\:)\:x(\:t\:+\:\tau\:)\:\mathrm{d}t \end{cases}

如果平稳过程使

\begin{cases}a\:=\:\overline{a}\\\\R(\:\tau\:)\:=\:\overline{R(\:\tau\:)}\end{cases}

成立。也就是说，平稳过程的统计平均值等于它的任一次实现的时间平均值，则称该平稳过程具有各态历经性。具有各态历经性的过程，其数字特征( 均为统计平均)完全可由随机过程中的任一实现的时间平均值来代替。

3.2.3 平稳过程的自相关函数

设 $\xi(t)$ 为实平稳随机过程，则它的自相关函数

R(\tau)\:=\:E[\:\xi(\:t)\:\xi(\:t\:+\:\tau)\:]

具有如下主要性质：

$R(0)=E[\xi^{2}(t)]$ ，表示 $\xi(t)$ 的平均功率。
$R(\tau)=R(-\tau)$ ,表示 $\tau$ 的偶函数。
$\mid R(\tau)\mid\leqslant R(0)$ ,表示 $R(\tau)$ 的上界。
$R( \infty) = E^{2}\left [ :\xi ( :t:) :\right ] = a^{2}$ ,表示 $\xi ( t )$ 的直流功率。
$R( 0) - R(\infty ) = \sigma ^2$ ， $\sigma^2$ 是方差，表示平稳过程 $\xi(t)$ 的交流功率。当均值为0 时，有 $R(0)=\sigma^2\circ$

3.2.4 平稳过程的功率谱密度

随机过程中的任一样本是一个确定的功率型信号。对于任意的确定功率信号 $f(t)$ ，它的功率谱密度定义为

P_f(f)\:=\:\lim_{T\to\infty}\frac{\mid F_T(f)\mid^2}{T}

式中 $:F_T(f)$ 为 $f(t)$ 的截短函数所对应的频谱函数。

我们不妨把 $f(t)$ 看成是平稳过程 $\xi(t)$ 的任一样本，过程的功率谱密度应看作是对所有样本的功率谱的统计平均，即

P_\xi(f)\:=\:E[\:P_f(f)\:]\:=\:\lim_{T\to\infty}\frac{E\mid\:F_T(f)\mid^2}{T}

平稳过程的功率谱密度 $P_{_{\epsilon}}(f)$ 与其自相关函数 $R(\tau)$ 也是一对傅里叶变换关系，即

\begin{cases} P_\xi(\:\omega\:)\:=\:\int_{-\infty}^{\infty}R(\:\tau\:)\:\mathrm{e}^{-\mathrm{j}\omega\tau}\:\mathrm{d}\tau\\ \\R(\:\tau\:)\:=\:\frac{1}{2\pi}\int_{-\infty}^{\infty}P_\xi(\:\omega\:)\:\mathrm{e}^{\mathrm{j}\omega\tau}\:\mathrm{d}\omega \end{cases}

以上关系称为维纳一辛钦( Wiener-Khinchine)定理。它在平稳随机过程的理论和应用中是一个非常重要的工具，它是联系频域和时域两种分析方法的基本关系式。

在维纳一辛钦关系的基础上，我们可以得到以下结论：

对功率谱密度进行积分，可以得到平稳过程的平均功率：

R\left(\begin{array}{c}0\end{array}\right)\:=\:\int_{-\infty}^{\infty}P_{\xi}\left(f\right)\mathrm{d}f

各态历经过程的任一样本函数的功率谱密度等于过程的功率谱密度。
功率谱密度 $P_\xi(f)$ 具有非负性和实偶性，即有
$P_{\xi}(f)\geq0$
和
$P_{\xi}(\:-f)\:=\:P_{\xi}(f)$
这与 $R(\tau)$ 的实偶性相对应。

3.3 高斯随机过程

高斯过程(Gaussian process),也称正态随机过程( normal random process),是通信领域中最重要也是最常见的一种过程。在实践中观察到的大多数噪声都是高斯型的，例如，通信系统中的主要噪声，即热噪声，就是一种高斯随机过程。

3.3.1定义

如果随机过程 $\xi(\iota)$ 的任意 $n$ 维 $(n=1,2,\cdots)$ 分布均服从正态分布，则称它为正态过程或高斯过程。其 $n$ 维正态概率密度函数表示如下：

f_n(\begin{array}{c}x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n\end{array})\\ =\frac{1}{\left(2\pi\right)^{n/2}\sigma_{1}\sigma_{2}\cdots\sigma_{n}\mid B\mid^{1/2}}\exp\Bigl[\frac{-1}{2\mid B\mid}\sum_{j=1}^{n}\sum_{k=1}^{n}\mid B\mid_{jk}\Bigl(\frac{x_{j}-a_{j}}{\sigma_{j}}\Bigr)\Bigl(\frac{x_{k}-a_{k}}{\sigma_{k}}\Bigr)\Bigr]

式中 $:a_k=E[\xi(t_{k})],\sigma_{k}^{2}=E\left[\xi(t_{k})-a_{k}\right]^{2};|B|$ 为归一化协方差矩阵的行列式，即

|B|=\begin{array}{c|ccccc|} &1&b_{12}&\cdots&b_{1n}\\\\ &b_{21}&1&\cdots&b_{2n}\\\\ &\vdots&\vdots&\cdots&\vdots\\ \\&b_{n1}&b_{n2}&\cdots&1 \end{array}

$|B|_{jk}$ 为行列式 $|\boldsymbol B|$ 中元素 $b_jk$ 的代数余因子； $b_jk$ 为归一化协方差函数，即

b_{jk}\:=\:\frac{E\mid\left[\:\xi(\:t_j\:)\:-\:a_j\:\right]\left[\:\xi(\:t_k\:)\:-\:a_k\:\right]\mid}{\sigma_j\sigma_k}

3.3.2 重要性质

高斯过程的 $n$ 维分布只依赖各个随机变量的均值、方差和归一化协方差。因此，对于高斯过程，只需要研究它的数字特征就可以了。
广义平稳的高斯过程也是严平稳的。因为，若高斯过程是广义平稳的，即其均值与时间无关，协方差函数只与时间间隔有关，而与时间起点无关，则它的 $n$ 维分布也与时间起点无关，故它也是严平稳的。所以，高斯过程若是广义平稳的，则也严平稳。
如果高斯过程在不同时刻的取值是不相关的，即对所有 $j\neq k$ 有 $b_{jk}=0$ ,这时n维概率密度函数可以简化为
$\begin{aligned}f_{n}(\:x_{1}\:,x_{2}\:,\cdots,x_{n}\:;t_{1}\:,t_{2}\:,\cdots,t_{n}\:)&=\prod_{k=1}^{n}\frac{1}{\sqrt{2\pi}\sigma_{k}}\exp\Big[\:-\:\frac{(\:x_{k}\:-\:a_{k}\:)^{2}}{2\sigma_{k}^{2}}\Big]\\&=f(\:x_{1}\:,t_{1}\:)\:\cdot f(\:x_{2}\:,t_{2}\:)\:\cdot\cdots\:\cdot f(\:x_{n}\:,t_{n}\:)\end{aligned}$
这表明，如果高斯过程在不同时刻的取值是不相关的，那么它们也是统计独立的。
高斯过程经过线性变换后生成的过程仍是高斯过程。

3.3.3 高斯随机变量

高斯过程在任一时刻上的取值是一个正态分布的随机变量，也称高斯随机变量，其一维概率密度函数为

f(\:x\:)\:=\:\frac{1}{\sqrt{2\pi}\sigma}\exp\Big(\:-\:\frac{(\:x\:-\:a\:)^2}{2\sigma^2}\Big)

式中： $a$ 和 $\sigma^2$ 分别为高斯随机变量的均值和方差； $f(x)$ 曲线如下图。

正态分布的概率密度 $f(x)$ 有以下特性：

$f(x)$ 对称于 $x=a$ 这条直线，即
$f(\:a\:+\:x\:)\:=f(\:a\:-\:x\:)$
积分面积为1
$\int_{-x}^{x}f( x ) \mathrm{d}x = 1\\ \int_{-x}^af( x ) \mathrm{d}x = \int_a^xf( x ) \mathrm{d}x = \frac{1}{2}$
$a$ 表示分布中心 $,\sigma$ 称为标准偏差，表示集中程度 $,f(x)$ 图形将随着 $\sigma$ 的减小而变高和变窄。当 $a=0,\sigma=1$ 时，称为标准化的正态分布，即
$f(x)\:=\:\frac{1}{\sqrt{2\pi}}\mathrm{exp}\Big(\:-\:\frac{x^2}{2}\Big)$

我们把正态分布的概率密度 $f(x)$ 积分定义为正态分布函数，它可表示为

F(\:x\:)\:=\:P(\:\xi\:\leqslant\:x\:)\:=\:\int_{-\infty}^{x}\:\frac{1}{\sqrt{2\:\pi}\:\sigma}\exp\Big[\:-\:\frac{(\:z\:-\:a\:)^{2}}{2\sigma^{2}}\Big]\mathrm{d}z

对于上式，令新积分变量 $t=(z-a)/\sqrt{2}\sigma$ ，有 d $z=\sqrt2\sigma dt$ ，则

F(\:x\:)\:=\:\frac{1}{2}\:\cdot\:\frac{2}{\sqrt{\pi}}\int_{-\infty}^{(\:x-a\:)/\sqrt{2}\:\sigma}\mathrm{e}^{-t^{2}}\mathrm{d}t\:=\:\frac{1}{2}\:+\:\frac{1}{2}\mathrm{erf}\Big(\:\frac{x-a}{\sqrt{2}\:\sigma}\Big)

式中：erf $(x)$ 表示误差函数，其定义为

\mathrm{erf}(\:x\:)\:=\:\frac{2}{\sqrt{\pi}}\:\int_0^x\mathrm{e}^{-t^2}\mathrm{d}t

它是自变量的递增函数，且有 $erf(0)=0,erf( \infty)=1,erf( -x)=-erf(x)$ 。 $F(x)$ 也可以用互补误差函数 erfc $(x)$ 表示，即

F(\:x\:)\:=\:1\:-\:\frac{1}{2}\mathrm{erfc}\Big(\:\frac{x\:-\:a}{\sqrt{2}\:\sigma}\Big)

式中：

\mathrm{erfc}(\:x\:)\:=\:1\:-\:\mathrm{erf}(\:x\:)\:=\:\frac{2}{\sqrt{\pi}}\int_{x}^{x}\mathrm{e}^{-t^{2}}\mathrm{d}t

$x>a$ ,互补误差函数与高斯概率密度函数曲线尾部下的面积成正比。当 $x$ 大时(实际应用中只要 $x>2$ ),互补误差函数可以近似为

\mathrm{erfc}(x) \approx \frac{1}{x\sqrt{\pi}}\mathrm{e}^{-x^2}

另一种经常用于表示高斯曲线尾部下的面积的函数记为 $Q(x)$ ,其定义为

Q(x)\:=\:\frac{1}{\sqrt{2\pi}}\int_{x}^{x}\mathrm{e}^{-t^{2}/2}\mathrm{d}t\quad x\geq0

和误差函数有如下性质

Q(\:x\:)\:=\:\frac{1}{2}\mathrm{erfc}\Big(\:\frac{x}{\sqrt{2}}\Big)\\ \mathrm{erfc}(\:x\:)\:=\:2Q(\:\sqrt{2}\:x\:)

$Q(x)$ 函数有如下性质：

Q(-x)=1-Q(x),x\geqslant0\\ Q(0)=\frac{1}{2}\text{及}Q(\infty)=0_{\circ}

3.4 平稳随机过程通过线性系统

线性时不变( time - invariant) 系统可由其单位冲激响应( unit impulse response ) $h(t)$ 或其频率响应 $H(f)$ 表征。若令 $v_i(t)$ 为输入信号， $v_o(t)$ 为输出信号，则输人与输出关系可以表示成卷积( convolution)，即

v_{o}(\:t\:)\:=\:v_{i}(\:t\:)\:*\:h(\:t\:)\:=\:\int_{-\infty}^{\infty}v_{i}(\:\tau\:)\:h(\:t\:-\:\tau\:)\:\mathrm{d}\tau

对应的傅里叶变换关系为

V_o(f)\:=\:H(f)\:V_i(f)

如果把 $v_i(t)$ 看作是输入随机过程的一个样本，则 $v_{\mathrm{o}}(t)$ 是输出随机过程的一个样本。输入输出也满足上式，即

\xi_{o}( t ) = \int_{-\infty}^{\infty}h( \tau ) \xi_{i}( t - \tau ) \mathrm{d}\tau

输出过程 $\xi_{\mathrm{o}}(t)$ 的均值
$E[\:\xi_{0}(\:t\:)\:]\:=\:E\left[\:\int_{-\infty}^{\infty}h(\:\tau\:)\:\xi_{i}(\:t\:-\:\tau\:)\:\mathrm{d}\tau\:\right]\:=\:\int_{-\infty}^{\infty}h(\:\tau\:)\:E[\:\xi_{i}(\:t\:-\:\tau\:)\:]\:\mathrm{d}\tau$
设输入过程是平稳的，则有 $E[\xi_i(t-\tau)]=E[\xi_i(t)]=a$ (常数)，所以
$E[\:\xi_{0}(\:t\:)\:]\:=\:a\:\cdot\:\int_{-\infty}^{\infty}h(\:\tau\:)\:\mathrm{d}\tau\:=\:a\:\cdot\:H(\:0\:)$
式中： $H(0)$ 为线性系统在 $f=0$ 处的频率响应，即直流增益。因此输出过程的均值， $E[\xi_0(t)]$ 是一个常数
输出过程 $\xi_{\mathrm{o}}(t)$ 的自相关函数 根据自相关函数的定义，输出过程的自相关函数为
$\begin{aligned}R_{_o}(\:t_{1}\:,t_{1}\:+\:\tau\:)&=\:E\bigl[\:\xi_{_o}\bigl(\:t_{_1}\bigr)\xi_{_o}\bigl(\:t_{_1}\:+\:\tau\bigr)\:\bigr]\\&=E\left[\int_{-\infty}^{\infty}h(\:\alpha\:)\xi_{i}(\:t_{1}\:-\:\alpha\:)\:\mathrm{d}\alpha\int_{-\infty}^{\infty}h(\:\beta\:)\xi_{i}(\:t_{1}\:+\:\tau\:-\:\beta\:)\:\mathrm{d}\beta\right]\\&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}h(\:\alpha\:)\:h(\:\beta\:)\:E[\:\xi_{i}(\:t_{1}\:-\:\alpha\:)\:\xi_{i}(\:t_{1}\:+\:\tau\:-\:\beta\:)\:]\:\mathrm{d}\alpha\mathrm{d}\beta\end{aligned}$
根据输入过程的平稳性，有
$E[\xi_i(\:t_1\:-\:\alpha\:)\xi_i(\:t_1\:+\:\tau\:-\:\beta\:)\:]\:=\:R_i(\:\tau\:+\:\alpha\:-\:\beta\:)$
于是
$R_{_o}(\:t_{_1}\:,t_{_1}\:+\:\tau)\:=\:\int_{_{-\infty}}^{\infty}\:\int_{_{-\infty}}^{\infty}h(\:\alpha\:)\:h(\:\beta\:)\:R_{_i}(\:\tau\:+\:\alpha\:-\:\beta\:)\:\mathrm{d}\alpha\mathrm{d}\beta\:=\:R_{_o}(\:\tau\:)$
输出过程的自相关函数仅仅是时间间隔 $\tau$ 的函数。若线性系统的输入过程是平稳的，那么输出过程也是平稳的。
输出过程 $\xi_{\mathrm{o}}(t)$ 的功率谱密度 对输出过程自相关函数进行傅里叶变换，有
$P_{_n}(f)\:=\:\int_{-x}^{\infty}R_{_o}(\:\tau\:)\:\mathrm{e}^{-\mathrm{j}\omega\tau}\:\mathrm{d}\tau\\ =\:\int_{-\infty}^{\infty}\:\left[\:\int_{-\infty}^{\infty}\:\int_{-\infty}^{\infty}h\left(\:\alpha\:\right)h\left(\beta\:\right)R\:\left(\:\tau\:+\:\alpha\:-\beta\:\right)\mathrm{d}\alpha\mathrm{d}\beta\:\right]\mathrm{e}^{-\mathrm{i}\omega\tau}\mathrm{d}\tau$
对上式进行变量代换，令 $\tau^\prime=\tau+\alpha-\beta$ ,则
$P_{_n}(f)\:=\:\int_{-\infty}^{\infty}h(\:\alpha\:)\:\mathrm{e}^{\mathrm{i}\omega\alpha}\:\mathrm{d}\alpha\:\int_{-\infty}^{\infty}h(\:\beta\:)\:\mathrm{e}^{-\mathrm{i}\omega\beta}\:\mathrm{d}\beta\:\int_{-\infty}^{\infty}R_{_i}(\:\tau^{\prime}\:)\:\mathrm{e}^{-\mathrm{i}\omega\tau^{\prime}}\:\mathrm{d}\tau^{\prime}$
即
$P_{_o}(f)\:=\:H^{*}(f)\:\cdot H(f)\:\cdot\:P_{_i}(f)\:=\mid\:H(f)\mid^{2}P_{_i}(f)$
输出过程的功率谱密度是输入过程的功率谱密度乘以系统频率响应模值的平方。当要求的是输出过程的自相关函数 $R_{_a}(\tau)$ 时，较容易的方法是先求功率谱密度 $P_o(\omega)$ ,然后计算其傅里叶反变换，这常常比直接计算 $R_o(\tau)$ 要简便得多。
输出过程 $\xi_0(t)$ 的概率分布 如果线性系统的输入过程是高斯型的，则系统的输出过程也是高斯型的。

3.5 窄带随机过程

若随机过程 $\xi(\iota)$ 的谱密度集中在中心频率 $f$ ，附近相对窄的频带范围 $\Delta f$ 内，即满足 $\Delta f\ll f$ 。条件，且 $f$ 。远离零频率，则称该 $\xi(t)$ 为窄带随机过程。频谱密度和波形如下图

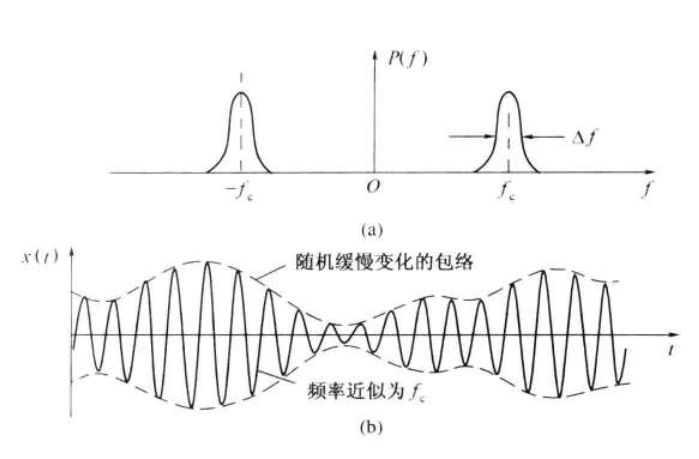
可见，窄带随机过程的一个样本的波形如同一个包络和相位随机缓变的正弦波。因此，窄带随机过程 $\xi(t)$ 可表示为

\xi(\:t\:)\:=\:a_{\xi}(\:t\:)\cos[\:\omega_{c}t\:+\varphi_{\xi}(\:t\:)\:]\quad a_{\xi}(\:t\:)\:\geqslant0

式中： $a_{\xi}(t)$ 及 $\varphi_{t}(\iota)$ 分别为窄带随机过程 $\xi(t)$ 的随机包络和随机相位； $\omega_c$ 为正弦波的中心角频率。进行三角函数展开，可以改写为

\xi(\:t\:)\:=\:\xi_{\mathrm{c}}(\:t\:)\cos\omega_{\mathrm{c}}t\:-\:\xi_{\mathrm{s}}(\:t\:)\sin\omega_{\mathrm{c}}t

其中

\xi_{c}(\:t\:)\:=\:a_{\xi}(\:t\:)\cos\varphi_{\xi}(\:t\:)\\ \xi_{s}(\:t\:)\:=\:a_{\xi}(\:t\:)\sin\varphi_{\xi}(\:t\:)

这里的 $\xi_c(t)$ 及 $\xi_s(t)$ 分别称为 $\xi(t)$ 的同相分量和正交分量。

假设 $\xi(t)$ 是一个均值为0，方差为 $\sigma_\xi^2$ 的平稳高斯窄带过程 , 我们来分析 $a_{\xi }( t) , \varphi _{\xi }( t)$ 及 $\xi_c(t),\xi_s(t)$ 的统计特性。

3.5.1 $\xi_c(t)$ 和 $\xi_s(t)$ 的统计特性

因为 $\xi(t)$ 平稳且均值为零，那么对于任意的时间 $t$ ，都有 $E[\xi(t)]=0$ ，则有

E[\:\xi(\:t\:)\:]\:=\:E[\:\xi_{c}(\:t\:)\:]\mathrm{cos}\omega_{c}t\:-\:E[\:\xi_{s}(\:t\:)\:]\mathrm{sin}\omega_{c}t=0

所以

E[\:\xi_{c}(t)\:]\:=\:0\:,\quad E[\:\xi_{s}(t)\:]\:=\:0

先计算 $\xi(t)$ 的自相关函数为

\begin{aligned} R_{\xi}(\:t\:,t\:+\:\tau\:)&=E[\:\xi(\:t\:)\xi(\:t\:+\:\tau\:)\:]\\&=R_{c}(\:t\:,t\:+\:\tau\:)\cos\omega_{c}t\cos\omega_{c}(\:t\:+\:\tau\:)\:-\:R_{cs}(\:t\:,t\:+\:\tau\:)\cos\omega_{c}t\sin\omega_{c}(\:t\:+\:\tau\:)\:-\\ &R_{sc}\left(t,t+\tau\right)sin\omega_ctcos\omega_c\left(t+\tau\right)+R_{s}\left(t,t+\tau\right)sin\omega_ctsin\omega_c\left(t+\tau\right) \end{aligned}

其中

R_{c}(t,t+\tau)=E\left[\xi_{c}(t)\xi_{c}(t+\tau)\right];R_{cs}(t,t+\tau)=E\left[\xi_{c}(t)\xi_{s}(t+\tau)\right]\\ R_{sc}\left(t,t+\tau\right)=E\left[\xi_{s}\left(t\right)\xi_{c}\left(t+\tau\right)\right];R_{s}\left(t,t+\tau\right)=E\left[\xi_{s}\left(t\right)\xi_{s}\left(t+\tau\right)\right]

因为 $\xi(t)$ 是平稳的，上式应与右端与时间 $t$ 无关，而仅与 $\tau$ 有关。因此，若令 $t=0$ ，上式变为

R_{\xi}(\tau)\:=\:R_{c}(\:t,t\:+\:\tau\:)\cos\omega_{c}\tau\:-\:R_{cs}(\:t,t\:+\:\tau\:)\sin\omega_{c}\tau

因与时间 $t$ 无关，以下两式自然成立：

R_{c}(\:t\:,t\:+\:\tau\:)\:=\:R_{c}(\:\tau\:)\:;R_{cs}(\:t\:,t\:+\:\tau\:)\:=\:R_{cs}(\:\tau\:)

所以

R_{\xi}(\tau)\:=\:R_{c}(\tau)\cos\omega_{c}\tau\:-\:R_{cs}(\tau)\sin\omega_{c}\tau

再令 $t=\frac\pi{2\omega_{c}}$ ,同理可求得

R_{\xi}(\:\tau\:)\:=\:R_{s}(\:\tau\:)\cos\omega_{c}\:\tau\:+\:R_{sc}(\:\tau\:)\sin\omega_{c}\tau

其中

R_{s}(t,t+\tau)=R_{s}(\tau);R_{sc}(t,t+\tau)=R_{sc}(\tau)

由以上分析可知，若窄带过程 $\xi(t)$ 是平稳的，则 $\xi_c(t)$ 与 $\xi_s(t)$ 也必然是平稳的。

同时可以看出

\begin{align} R_{_c}( \tau )&= R_{_s}( \tau )\\R_{cs}( \tau )&=- R_{sc}( \tau ) \end{align}

因此 $R_{sc}(\tau)$ 和 $R_{cs}(\tau)$ 都是 $\tau$ 的奇函数，所以

R_{_{\mathrm{sc}}}\left(0\right)&=0\\ R_{_{\mathrm{cs}}}\left(0\right)&=0

于是

R_{\xi}(\:0\:)\:=\:R_{c}(\:0\:)\:=\:R_{s}(\:0\:)

即

\sigma_{\xi}^{2}\:=\:\sigma_{c}^{2}\:=\:\sigma_{s}^{2}

因为 $\xi(t)$ 是高斯过程，所以 $\xi_c(t_1),\xi_s(t_2)$ 一定是高斯随机变量，从而 $\xi_{\mathrm{c}}(t),\xi_{\mathrm{s}}(t)$ 也是高斯过程。根据式 $R_{{\mathrm{cs}}}\left(0\right)=0$ 可知$$xi{\mathrm{c}}(t)$$，与 $\xi_{\mathrm{s}}(t)$ 在 $\tau=0$ 处互不相关，又由于它们是高斯型的，因此 $\xi_{\circ}(t)$ 与 $\xi_{,}(t)$ 也统计独立。

综上所述，我们得到一个重要结论：一个均值为零的窄带平稳高斯过程 $\xi(t)$ ,它的同相分量 $\xi_c(t)$ 和正交分量 $\xi_s(t)$ 同样是平稳高斯过程，而且均值为零，方差也相同。此外，在同一时刻上得到的 $\xi_c$ 。和 $\xi_s$ 是互不相关的或统计独立的。

3.5.2 $a_\xi(t)$ 和 $\varphi(t)$ 的统计特性

由上面的分析可知， $\xi_c$ 和 $\xi_s$ 的联合概率密度函数为

f(\xi_{c},\xi_{s})\:=f(\xi_{c})\:\cdot f(\xi_{s})\:=\:\frac{1}{2\pi\sigma_{\xi}^{2}}\mathrm{exp}\Big[\:-\:\frac{\xi_{c}^{2}\:+\:\xi_{s}^{2}}{2\sigma_{\xi}^{2}}\Big]

设 $a_\xi,\varphi_\xi$ 的联合概率密度函数为 $f(a_\xi,\varphi_\xi)$ ，则根据概率论知识有

f(\:a_{\xi},\varphi_{\xi})\:=f(\:\xi_{c},\xi_{s})\:\left|\:\frac{\partial(\:\xi_{c},\xi_{s})}{\partial(\:a_{\xi},\varphi_{\xi})}\:\right|

又

\begin{cases}\xi_c&=&a_\xi\mathrm{cos}\varphi_\xi\\\\\xi_s&=&a_\xi\mathrm{sin}\varphi_\xi\end{cases}

可以求得

\left|\frac{\partial(\xi_c,\xi_s)}{\partial( a_\xi,\varphi_\xi)}\right| = \begin{array} {|cc|} \frac{\partial\xi_c}{\partial a_\xi} &\frac{\partial\xi_s}{\partial a_\xi}\\ \frac{\partial\xi_c}{\partial\varphi_\xi} &\frac{\partial\xi_s}{\partial\varphi_\xi} \end{array} =\begin{array} {|cc|} \cos\varphi_\xi &\sin\varphi_\xi\\ -a_\xi\sin\varphi_\xi &a_\xi\cos\varphi_\xi \end{array}=a_\xi

于是

\begin{aligned} f(\:a_{\xi}\:,\varphi_{\xi}\:) &=\:a_{\xi}f(\:\xi_c\:,\xi_s\:)\: =\:\frac{a_{\xi}}{2\pi\sigma_{\xi}^{2}}\exp\Big[\:-\:\frac{(\:a_{\xi}\mathrm{cos}\varphi_{\xi}\:)^{2}\:+\:(\:a_{\xi}\mathrm{sin}\varphi_{\xi}\:)^{2}}{2\sigma_{\xi}}\Big] \\&=\:\frac{a_{\xi}}{2\pi\sigma_{\xi}^{2}}\mathrm{exp}\Big[\:-\:\frac{a_{\xi}^{2}}{2\sigma_{\xi}^{2}}\Big]\end{aligned}

再利用概率论中的边际分布关系，将 $f(a_\xi,\varphi_\xi)$ 对 $\varphi_\xi$ 积分求得包络 $a_\xi$ 的一维概率密度函数为

\begin{aligned}f(\:a_{\xi}\:)&=\:\int_{-\infty}^{\infty}f(\:a_{\xi},\varphi_{\xi}\:)\:\mathrm{d}\varphi_{\xi}\:=\:\int_{0}^{2\pi}\:\frac{a_{\xi}}{2\:\pi\sigma_{\xi}^{2}}\mathrm{exp}\Big[\:-\:\frac{a_{\xi}^{2}}{2\sigma_{\xi}^{2}}\Big]\mathrm{d}\varphi_{\xi}\\&=\:\frac{a_{\xi}}{\sigma_{\xi}^{2}}\mathrm{exp}\Big[\:-\:\frac{a_{\xi}^{2}}{2\sigma_{\xi}^{2}}\Big]\quad a_{\xi}\geqslant0\end{aligned}

可见， $a_{\xi}$ 服从瑞利( Rayleigh)分布。

由 $f(a_\xi,\varphi_\xi)$ 对 $a_\xi$ 积分求得相位 $\varphi_\xi$ 的一维概率密度函数

\begin{aligned}f(\:\varphi_{\xi}\:)&=\:\int_{0}^{\infty}f(\:a_{\xi},\varphi_{\xi}\:)\:\mathrm{d}a_{\xi}\\&=\:\frac{1}{2\pi}\int_{0}^{\infty}\:\frac{a_{\xi}}{\sigma_{\xi}^{2}}\mathrm{exp}\biggl(\:-\:\frac{a_{\xi}^{2}}{2\sigma_{\xi}^{2}}\biggr)\mathrm{d}a_{\xi}\:=\:\frac{1}{2\pi}\:0\:\leqslant\:\varphi_{\xi}\:\leqslant\:2\:\pi\end{aligned}

可见， $\varphi_\xi$ 服从均匀分布

综上所述，我们又得到一个重要结论：一个均值为零、方差为 $\sigma_\xi^2$ 的窄带平稳高斯过程 $\xi(t)$ ,其包络 $a_\xi(t)$ 的一维分布是瑞利分布，相位 $\varphi_\xi(t)$ 的一维分布是均匀分布，并且就一维分布而言， $a_\xi(t)$ 与 $\varphi_\xi(t)$ 是统计独立的，即

f(\:a_{\xi},\varphi_{\xi}\:)\:=f(\:a_{\xi}\:)\:\cdot f(\:\varphi_{\xi}\:)

3.6 正弦波加窄带高斯噪声

设正弦波加窄带高斯噪声的混合信号为

r(\:t\:)\:=\:A\cos(\:\omega_{\mathrm{c}}t\:+\:\theta\:)\:+\:n(\:t\:)

式中： $n(t)=n_{c}(t)\cos\omega_{c}t-n_{s}(t)\sin\omega_{c}t$ ，为窄带高斯噪声，其均值为零，方差为 $\sigma_n^2;\theta$ 为正弦波的随机相位，在(0,2π)上均匀分布；振幅 $A$ 和角频率 $\omega_{\circ}$ 均假定为确知量。

于是

\begin{align} r(\:t\:)\:&=\:\left[\:A\mathrm{cos}\theta\:+\:n_{c}(\:t\:)\:\right]\mathrm{cos}\omega_{c}t\:-\:\left[\:A\mathrm{sin}\theta\:+\:n_{s}(\:t\:)\:\right]\mathrm{sin}\omega_{c}t\\ &=\:z_{c}\left(\:t\:\right)\mathrm{cos}\omega_{c}t\:-\:z_{s}\left(\:t\:\right)\mathrm{sin}\omega_{c}t\\ &=\:z(\:t\:)\cos\bigl[\:\omega_{c}t\:+\:\varphi(\:t\:)\:\bigr]\\ \end{align}

其中

\begin{align} &z_{c}\left(\:t\:\right)\:=\:A\mathrm{cos}\theta\:+\:n_{c}\left(\:t\:\right) \\&z_{s}\left(\:t\:\right)\:=\:A\mathrm{sin}\theta\:+\:n_{s}\left(\:t\:\right) \end{align}

$r(t)$ 的包络和相位分别为

z(\:t\:)\:=\:\sqrt{z_{c}^{2}(\:t\:)\:+z_{s}^{2}(\:t\:)}\quad z\geqslant0\\\varphi(\:t\:)\:=\:\arctan\frac{z_{s}(\:t\:)}{z_{c}(\:t\:)}\quad0\leqslant\varphi\leqslant2\pi

如果 $\theta$ 值已给定，则 $z_{{\mathrm{c}}},z{_{\mathrm{s}}}$ 是相互独立的高斯随机变量，且有

E[\:z_c\:]\:=\:A\mathrm{cos}\theta;E[\:z_s\:]\:=\:A\mathrm{sin}\theta;\sigma_c^2\:=\:\sigma_s^2\:=\:\sigma_n^2

所以，在给定相位 $\theta$ 的条件下的 $z$ 和 $\varphi$ 的联合概率密度函数为

f(z_{e},z_{s}/\theta)\:=\:\frac{1}{2\pi\sigma_{n}^{2}}\mathrm{exp}\Big\{-\frac{1}{2\sigma_{n}^{2}}\Big[\:(z_{e}\:-A\mathrm{cos}\theta)^{2}\:+\:(z_{s}\:-A\mathrm{sin}\theta)^{2}\Big]\Big\}

其中

z_{c}\:=\:z\mathrm{cos}\varphi\:;z_{s}\:=\:z\mathrm{sin}\varphi

可以求得在给定相位 $\theta$ 的条件下的 $z$ 与 $\varphi$ 的联合概率密度函数为

\begin{aligned}f(z,\varphi/\theta)&=f(z_{c},z_{s}/\theta)\:\bigg|\frac{\partial(z_{c}z_{s})}{\partial(z,\varphi)}\bigg|\:=\:z\cdot f(z_{c},z_{s}/\theta)\\&=\frac{z}{2\pi\sigma_{n}^{2}}\mathrm{exp}\Big\{-\frac{1}{2\sigma_{n}^{2}}\Big[\:z^{2}\:+\:A^{2}\:-\:2Az\mathrm{cos}(\:\theta\:-\:\varphi\:)\:\Big]\:\Big\}\end{aligned}

然后求给定 $\theta$ 条件下的边际分布，即

\begin{aligned}f(\:z/\theta\:)&=\:\int_{0}^{2\pi}f(\:z\:,\varphi/\theta\:)\:\mathrm{d}\varphi\\&=\:\frac{z}{2\:\pi\sigma_{n}^{2}}\mathrm{exp}\Big(\:-\:\frac{z^{2}\:+\:A^{2}}{2\sigma_{n}^{2}}\Big)\cdot\:\int_{0}^{2\pi}\mathrm{exp}\Big[\:\frac{Az}{\sigma_{n}^{2}}\mathrm{cos}\:(\:\theta\:-\:\varphi\:)\:\Big]\mathrm{d}\varphi\end{aligned}

由于

\frac{1}{2\pi}\int_{0}^{2\pi}\exp[\:x\cos\varphi\:]\:\mathrm{d}\varphi\:=\:I_{0}(\:x\:)

故有

\frac{1}{2\pi}\int_{0}^{2\pi}\exp\Bigl[\frac{Az}{\sigma_{n}^{2}}\mathrm{cos}(\:\theta-\varphi\:)\:\Bigr]\mathrm{d}\varphi\:=\:I_{0}\Bigl(\frac{Az}{\sigma_{n}^{2}}\Bigr)

式中 $:I_0(x)$ 为第一类零阶修正贝塞尔函数

当 $x\geqslant0$ 时， $I_{0}(x)$ 是单调上升函数，且有 $I_{0}(0)=1$ ，因此

f(\:z/\theta\:)\:=\:\frac{z}{\sigma_n^2}\:\cdot\:\exp\Big[\:-\:\frac{1}{2\sigma_n^2}(\:z^2\:+\:A^2\:)\:\Big]I_0\Big(\frac{Az}{\sigma_n^2}\Big)

由上式可见 , $f(z/\theta)$ 与 $\theta$ 无关 ,故 $r(t)$ 的包络 $z$ 的概率密度函数为

f(\:z\:)\:=\:\frac{z}{\sigma_{n}^{2}}\mathrm{exp}\Big[\:-\frac{1}{2\sigma_{n}^{2}}(\:z^{2}\:+\:A^{2}\:)\:\Big]I_{0}\Big(\frac{Az}{\sigma_{n}^{2}}\Big)\quad z\geqslant0

这个概率密度函数称为广义瑞利分布，又称莱斯( Rice)分布。

存在两种极限情况：

当信号很小，即 $A\to0$ 时，信号功率与噪声功率的比值 $\gamma=\frac{A^2}{2\sigma_n^2}\to0$ ,相当于$x$值很小，于是有 $I_0(x)=1$ ,由莱斯分布退化为瑞利分布。
当信噪比 $\gamma=\frac{A^2}{2\sigma^2}$ 很大时，有 $I_0(x)\approx\frac{\mathrm{e}^x}{\sqrt{2\pi x}}$ ,这时在 $z\approx A$ 附近 $,f(z)$ 近似为高斯分布，即
$f(z)\:\approx\frac{1}{\sqrt{2\pi}\sigma_n}\cdot\exp\Big(\:-\:\frac{(\:z\:-\:A\:)^2}{2\sigma_n^2}\Big)$

由此可见，正弦波加窄带高斯噪声的包络分布 $f(z)$ 与信噪比有关。小信噪比时， $f(z)$ 接近于瑞利分布；大信噪比时 $,f(z)$ 接近于高斯分布；在一般情况下， $f(z)$ 才是莱斯分布。

3.7 高斯白噪声和带限白噪声

白噪声
白噪声的功率谱密度在所有频率上均为一常数，双边功率谱密度为
$P_{_n}(f) = \frac{n_0}{2}\quad( - \infty <f <+ \infty )\quad( \mathrm{W/Hz} )$
单边功率谱密度为
$P_n(f)\:=\:n_0\quad(\:0\:<f\:<\:+\:\infty\:)\quad(\:\mathrm{W/Hz}\:)$
白噪声的自相关函数为
$R(\:\tau\:)\:=\:\frac{n_0}{2}\delta(\:\tau\:)$
如图1，对于所有的 $\tau\neq0$ 都有 $R(\tau)=0$ ,这表明白噪声仅在 $\tau=0$ 时才相关，而在任意两个时刻( 即 $\tau\neq0$ )的随机变量都是不相关的。
由于白噪声的带宽无限，其平均功率为无穷大，即
$R(0)\:=\:\int_{-\infty}^{x}\:\frac{n_{0}}{2}\mathrm{d}f\:=\:\infty$
或
$R(0)\:=\:\frac{n_0}{2}\delta(0)\:=\:\infty$
因此，真正“白”的噪声是不存在的，它只是构造的一种理想化的噪声形式，其中“白”和白光中的“白”有相同的意思；白光指在电磁辐射可见范围内所有频率分量的数值都相等。
如果白噪声取值的概率分布服从高斯分布，则称为高斯白噪声，我们常用它作为通信信道中的噪声模型。高斯白噪声在任意两个不同时刻上的随机变量之间，不仅是互不相关的，而且还是统计独立的
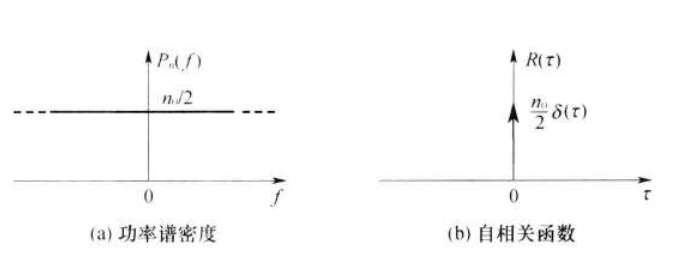
图1
低通白噪声
如果白噪声通过理想矩形的低通滤波器或理想低通信道，则输出的噪声称为低通( lowpass)白噪声，也用 $n(t)$ 表示。低通白噪声对应的功率谱密度为
$P_n(f) = \begin{cases}\frac{n_0}{2}&| f|\leqslant f_H\\\\0&\text{其他}\end{cases}$
自相关函数为
$R(\:\tau\:)\:=\:n_0f_H\:\frac{\sin2\pi f_H\tau}{2\pi f_H\tau}$
对应曲线如下图2
这种带限白噪声只有在 $\tau=k/2f_{H}(k=1,2,3,\cdots)$ 上得到的随机变量才不相关。也就是说，如果按抽样定理对带限白噪声进行抽样的话，各抽样值是互不相关的随机变量。这是一个很重要的概念。
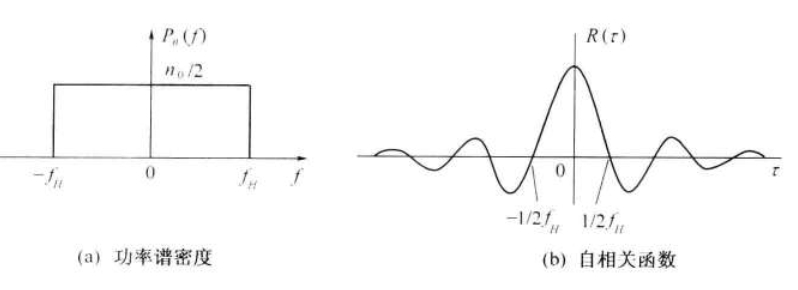
图2
带通白噪声
如果白噪声通过理想矩形的带通( bandpass)滤波器或理想带通信道，则其输出的噪声称为带通白噪声，仍用 $n(t)$ 表示。带通噪声的功率谱密度为
$P_n(f)\:=\:\begin{cases}\dfrac{n_0}{2}&f_c\:-\dfrac{B}{2}\leqslant\mid f\mid\leqslant f_c\:+\dfrac{B}{2}\\\\0&\text{其他}\end{cases}$
自相关函数为
$\begin{aligned}R(\:\tau\:)&=\:\int_{-\infty}^{\infty}P_{n}\left(f\right)\mathrm{e}^{j2\pi f\tau}\mathrm{d}f\:=\:\int_{-f_{c}-\frac{B}{2}}^{-f_{c}+\frac{B}{2}}\frac{n_{0}}{2}\mathrm{e}^{j2\pi f\tau}\mathrm{d}f\:+\:\int_{f_{c}-\frac{B}{2}}^{f_{c}+\frac{B}{2}}\frac{n_{0}}{2}\mathrm{e}^{j2\pi f\tau}\mathrm{d}f\\&=\:n_{0}B\:\frac{\sin\pi B\tau}{\pi B\tau}\mathrm{cos}2\pi f_{c}\tau\end{aligned}$
对应的曲线如图3
通常，带通滤波器的 $B\ll f_c$ ,因此也称窄带( narrowband)滤波器，相应地把带通白噪声称为窄带高斯白噪声，因此它的表达式和统计特性与一般窄带随机过程相同。 $n(t)$ 的平均功率为
$N = n_{0}B$
图3