🫔5. 模拟调制系统
调制:把消息信号搭载到载波的某个参数上
载波:一种高频周期振荡信号,如正弦波,受调载波称为已调信号,含有消息信号特征
解调:调制的逆过程,从已调信号中恢复消息信号
调制的目的:
进行频谱搬移,匹配信道特性,减小天线尺寸
实现多路复用,提升信道利用率
改善系统性能
实现频率分配
调制的分类:
按调制信号m(t)的类型
模拟调制
数字调制
按已调信号的频谱结构分
线性调制
非线性调制
按正弦载波的受调参量分
幅度调制
频率调制
相位调制
按载波信号c(t)的类型分
连续波调制
脉冲调制
5.1 幅度调制(线性调制)的原理
一般模型

5.1.1 常规调幅(AM)
AM调制器
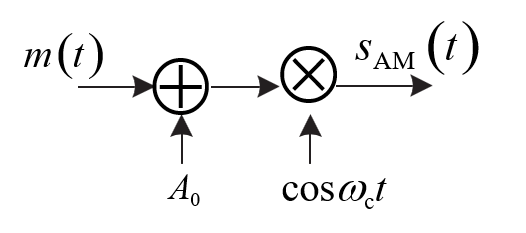
第一项为载波项,第二项为边带项。
调制信号要满足:
转换到频域:
AM波形和频谱如下:
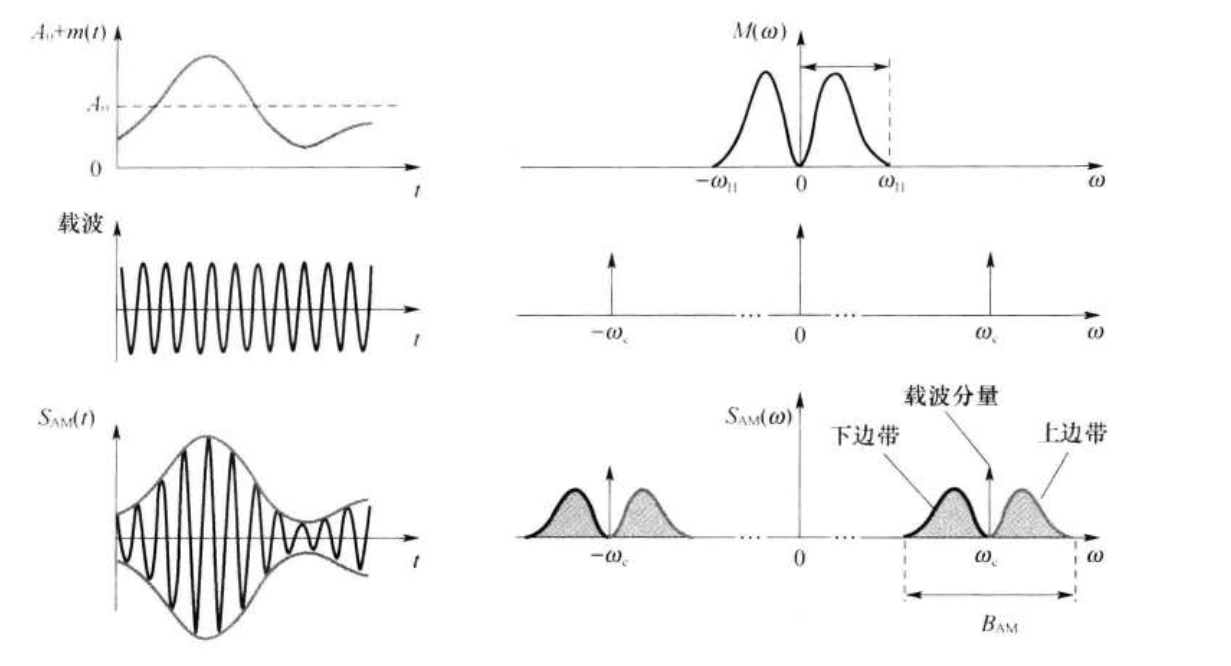
AM信号的特点:
∣m(t)∣max≤A0时,AM波的包络正比于调制信号m(t),故可采用包络检波
AM的频谱由载频分量,上边带和下边带组成
AM的传输带宽是调制信号带宽的两倍,BAM=2fH
AM的优势在于接收机简单,广泛用于中短调幅广播
AM信号功率:
其中,Pc为载波功率,Ps为边带功率
调制效率(功率利用率):
所以AM信号的缺点是功率利用率低。
定义:调幅系数m(用百分比表示,又称调幅度),反映基带信号改变载波幅度的程度
m<1,正常调幅
m>1,过调幅
m=1,临界状态,满调幅

当m=1(满调幅)时,AM调制效率的最大值仅为1/3,可见AM的功率利用率很低。
5.1.2 抑制载波双边带调制(DSB-SC)
DSB调制器

调制信号满足:
DSB波形和频谱如下:

DSB信号的特点:
包络不再与m(t)成正比,当m(t)改变符号时,载波相位反转,故不能采用包络检波,需相干解调
带宽与AM相同:BDSB=BAM=2fH
调制效率100%,即功率利用率高
无载频分量,只有上、下边带
主要用作单边带调制(SSB)、残留边带调制(VSB)的技术基础,以及调频立体声的差信号调制等
5.1.3 单边带调制(SSB)
SSB信号的产生
滤波法

原理:先生成DSB信号,边带滤波即得上或下边带信号
要求:滤波器HSSB(ω)在载频处具有陡峭的截至特性,如图

滤波后的频带如图
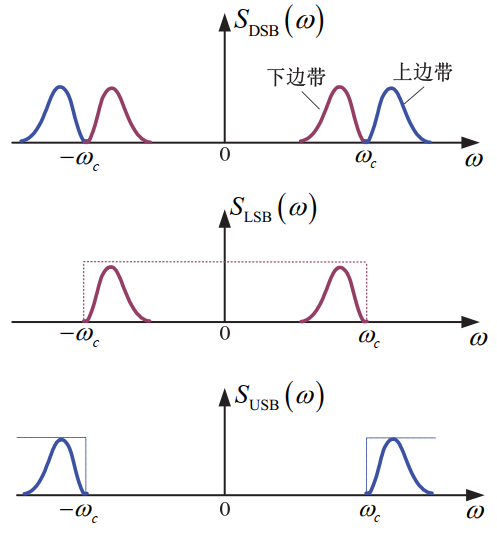
相移法
设m(t)=Amcosωmt,载波c(t)=cosωct,则
SDSB(t)=Amcosωmt⋅cosωct=21Amcos(ωc−ωm)t+21Amcos(ωc+ωm)t则
LLSB(t)=21Amcos(ωc−ωm)t=21Amcosωmtcosωct+21Amsinωmtsinωct=21m(t)cosωct+21m(t)^sinωctLUSB(t)=21Amcos(ωc+ωm)t=21Amcosωmtcosωct−21Amsinωmtsinωct=21m(t)cosωct−21m(t)^sinωct其中m(t)^是m(t)的希尔伯特变换,m(t)^=Amsinωmt,含义:幅度不变,相移π/2,希尔伯特变换的传输函数:
M(ω)=Hh(ω)⋅M(ω)Hh(ω)=M(ω)M(ω)^=−jsgnωsgnω={1,−1,ω>0ω<0要求:H(ω)对m(t)的所有频率分量精确相移π/2。

SSB信号的特点:
频带利用率高
其传输带宽仅为AM/DSB的一半:$B_{SSB}=B_{AM/2}=f_H$
因此在频谱拥挤的通信场合获得了广泛应用,尤其在短波通信和多路载波电话中占有重要地位
低功耗特性
因为不需要传送载波和另一个边带而节省了功率,低功耗对移动通信尤为重要
缺点:设备复杂,存在技术难点
5.1.4 残留边带调制
这是介于SSB和DSB之间的折中方案。
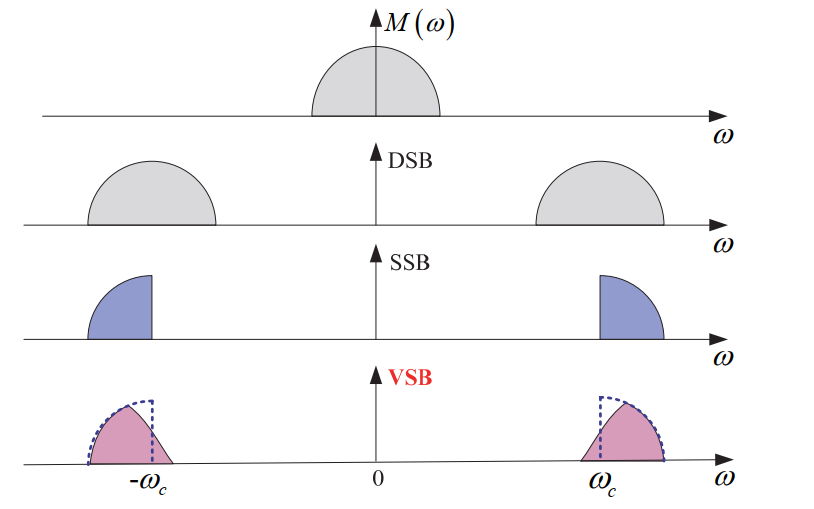
VBS信号的产生:

VSB信号的解调:
如图:
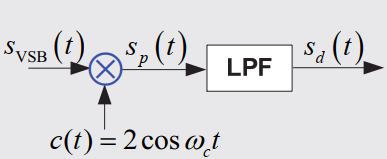
其中
因此LPF的解调输出为:
若要无失真恢复m(t),VSB滤波器的传输函数必须满足:
含义:在载频处具有互补对称特性(奇对称)
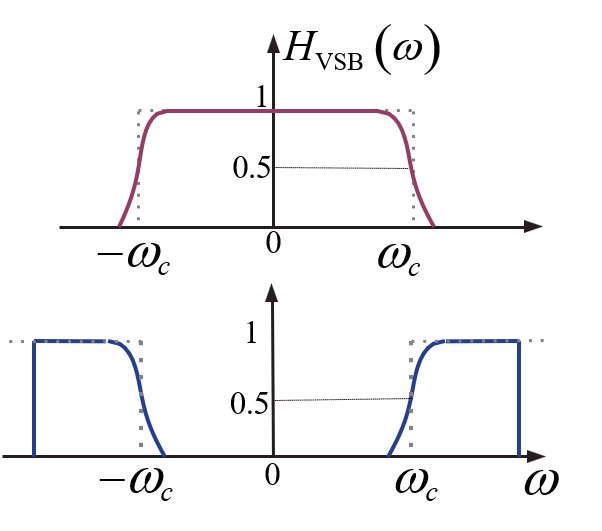
VBS信号的特点:
仅比SSB所需带宽有很小的增加,却带来了电路的简化 fH<BVSB<2fH
应用:商业电视广播中电视信号传输。
5.1.5 线性调制(幅度调制)的一般模型
滤波法
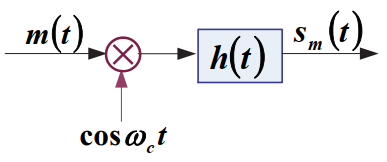
相移法
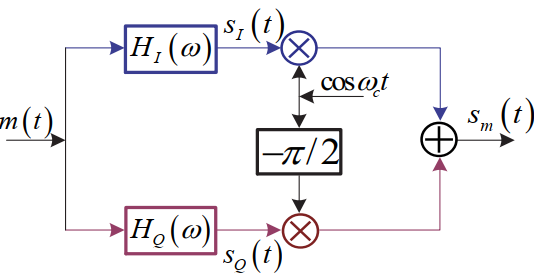
5.1.6 相干解调和包络检波
相干解调
适用:AM、DSB、SSB、VSB
特点:无门限效应(克服包络检波的缺点)
要求:需要一个与接收到的已调载波严格同步的本地载波(相干载波)
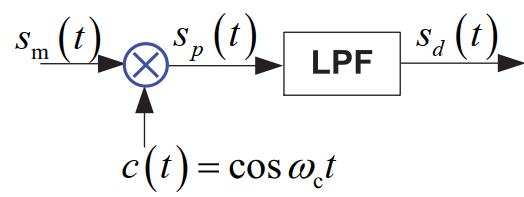
包络检波
适用:AM信号
优势:简单、无需载波同步
要求:∣m(t)∣max≤A0

插入载波包络检波法
适用:DSB、SSB或VSB等抑制载波的已调信号
原理:将这些信号插入恢复载波,使之成为或近似成为AM信号,然后用包络检波器恢复出m(t)
要求:Ad很大(功率效率低)、载波同步
方法:发端或收端认为插入强载波

5.2 线性调制系统的抗噪声性能
5.2.1 模型和指标
分析模型:
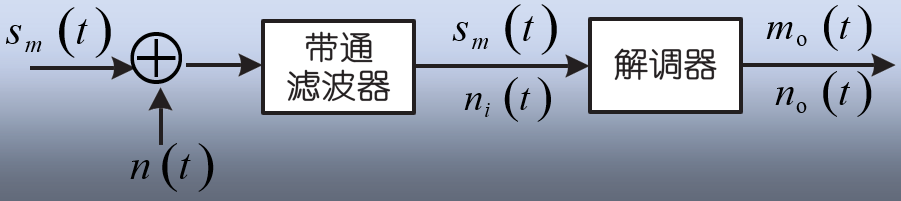
其中,sm(t)是已调信号,n(t)是信道加性白噪声,带通滤波器的作用是滤除已调信号频带以外的噪声,因此经过带通滤波器到达解调器输入端的信号仍可认为是sm(t),而噪声是ni(t),解调器输出的有用信号为mo(t),噪声为no(t)。
当带通滤波器的带宽远小于其中心频率,可以视为窄带滤波器,所以ni(t)为平稳窄带高斯噪声,它的表达式为
则解调器输入噪声的平均功率为
性能指标:
解调器输出信噪比:
NoSo=no2(t)mo2(t)解调器输入信噪比:
NiSi=ni2(t)si2(t)调制制度增益:
G=Si/NiSo/No
5.2.2 DSB-相干解调系统的抗噪声性能

设解调器的输入信号为:
解调器输入信号的平均功率为:
与相干载波cosωct相乘后,得
经过低通滤波器后,输出信号为
所以解调输出端有用信号功率为
解调器输入端的窄带高斯噪声ni(t)可表示为
它与相干载波cosωct相乘后,得
经过低通滤波器后,解调器最终输出的噪声为
故输出的噪声功率为
由上可得,解调器的输入信噪比为
输出信噪比为
制度增益为
SNR增加的原因:相干解调将噪声ni(t)中的正交分量抑制掉,从而使信噪比改善1倍
5.2.3 SSB-相干解调系统的抗噪声性能
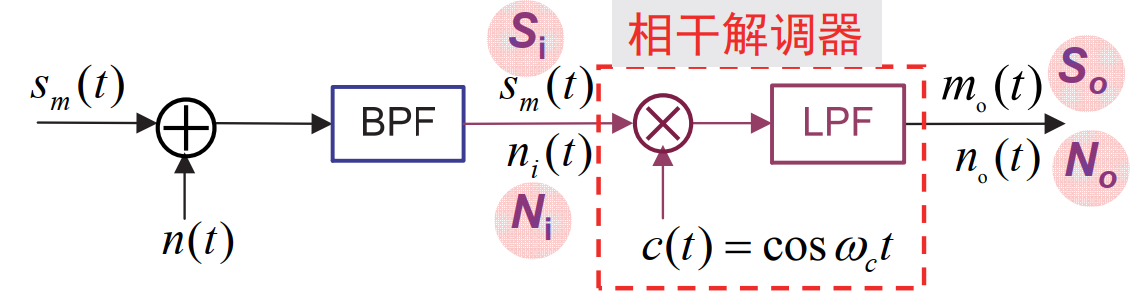
解调器的输入信号为:
解调器输入信号功率为:
解调器输出信号为:
输出信号功率为:
输入输出噪声功率为:
由上可知
因此
SSB的SNR没有增加的原因是相干解调抑制正交分量(无论信号还是噪声)。GDSB=2GSSB不能说明DSB系统的抗噪声性能比SSB系统好,对于这两种调制方式,可以发现它们的输出信噪比是相等的,也就是说两者的抗噪声性能是相同的。但SSB所需要的带宽仅是DSB的1/2,因此SSB得到普遍应用。
5.2.4 AM-包络检波系统的抗噪声性能

设解调器输入信号为
解调器输入噪声为
解调器输入信号功率为
输入噪声功率为
输入信噪比为
解调器的输入是信号加噪声的混合波形,即
其中,E(t)便是所求的合成包络
考虑两者特殊情况:
大信噪比时
输入信号幅度远大于噪声幅度,即
[A0+m(t)]>>nc2(t)+ns2(t)则E(t)可简化为
E(t)≈A0+m(t)+nc(t)当直流分量A0被电容器阻隔后,有用信号与噪声信号独立分成两项,因而可以分别计算它们的功率
S0=m02(t)=m2(t)No=nc2(t)=Ni输出信噪比为
NoSo=n0Bm2(t)调制制度增益为
GAM=Si/NiSo/No=A02+m2(t)2m2(t)讨论:
由于∣m(t)∣max≤A0,所以$$G{AM}<1$$,即$$\frac{S_o}{N_o}<\frac{S_i}{N_i}$$
100%调制,且m(t)为单频正弦信号时,GAM=32
相干解调的GAM如同上式,但可以不受信噪比条件的限制,即避免了门限效应
小信噪比时
[A0+m(t)]<<nc2(t)+ns2(t)E(t)可以简化为
E(t)=R(t)+[A0+m(t)]cosθ(t)其中,R(t)=nc2(t)+ns2(t),θ(t)=arctannc(t)ns(t)
可见,小信噪比时,信号被扰乱成噪声,导致信噪比急剧恶化——门限效应
5.3 非线性调制(角度调制)原理
概述:
FM和PM的总称
载波的幅度恒定,而频率或相位受调制
属于非线性调制
抗噪声性能优于幅度调制
5.3.1 角度调制的基本概念
角度调制的一般表达式
式中,A为恒定振幅,[ωct+ϕ(t)]为信号的瞬时相位,记为θ(t),φ(t)为相对于载波相位ωct的瞬时相位偏移,d[ωct+φ(t)]/dt为信号的瞬时角频率,记为ω(t),dφ(t)/dt为相对于载频$\omega_c$的瞬时频偏。
相位调制(PM)
φ(t)=Kpm(t)调相灵敏度为
Kp=rad/V调相表达式为
SPM(t)=Acos[ωct+Kpm(t)]频率调制(FM)
dtdφ(t)=Kfm(t)调频灵敏度为
Kf=rad/(s⋅V)调频表达式为
sFM(t)=Acos[ωct+Kf∫m(τ)dτ]
PM与FM的关系:
PM是相位偏移随m(t)作线性变化
FM是相位偏移随m(t)的积分作线性变化
若预先不知m(t)的形式,不能判断已调信号是PM还是FM信号。
5.3.2&5.3.3 窄带调频&宽带调频
若最大瞬时相位偏移满足:
则为窄带调频(NBFM);否则为宽带调频(WBFM)
单音调频FM
设m(t)=Amcosωmt,则dtdφ(t)=KfAmcosωmt,则
φ(t)=KfAm∫cosωmtdt=ωmKfAmsinωmt=mfsinωmt所以单音调频信号
SFM(t)=Acos[ωct+mfsinωmt]调频指数为
mf=ωmKfAm=ωmΔω=fmΔfFM信号的频谱与带宽
对单音频信号进行级数展开,有
sFM(t)=An=−∞∑∞Jn(nf)cos(ωc+nωm)t其中Jn为第一类n阶贝塞尔函数,是调频指数mf的函数。
进行傅里叶变换,有
SFM(ω)=πA−∞∑∞Jn(mf)[δ(ω−ωc−nωm)+δ(ω+ωc+nωm)]讨论:
载频分量ωc和无数多对边频ωc±nωm(分布在ωc两侧)
边频幅度Jn(mf)随着n增大而逐渐减小
工程上:保留上下边频分量共有2n=2(mf+1)个,相邻边频之间的频率间隔为fm,所以FM的带宽近似为:
BFM=2(mf+1)fm=2(Δf+fm)mf<<1时,BFM≈2fm,为窄带调频(NBFM)
mf>>1时,BFM≈2Δf,宽带调频(WBFM)
推广:对于多音或任意带限调制信号时的FM信号:
BFM=2(mf+1)fm=2(Δf+fm)式中,fm为调制信号的最高频率
FM信号的功率分配
SFM(t)=An=−∞∑∞Jn(mf)cos(ωc+nωm)t根据帕塞瓦尔定理
PFM=SFM2(t)=2A2n=−∞∑∞Jn2(mf)=2A2=Pc根据贝塞尔函数有
n=−∞∑∞Jn2(mf)=1因此
PFM=2A2=Pc该式说明,调制后总的功率不变,只是将载波功率重新分配给边频分量,而功率分配的比例与调频指数mf有关
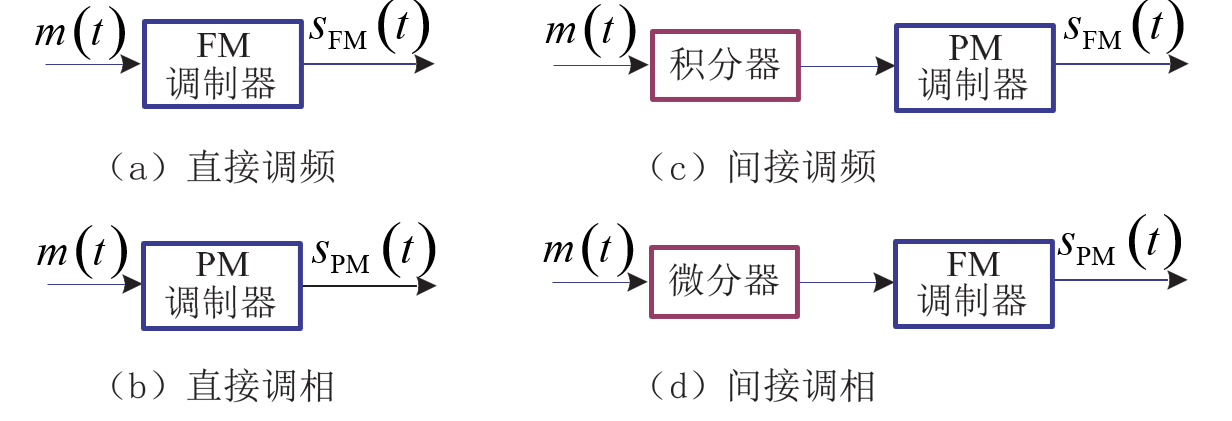
5.3.4 调频信号的产生与解调
调频信号的产生
直接法
原理:调制压控振荡器的频率
ωi(t)=ω0+Kfm(t)优点:电路简单,可获得较大频偏
缺点:频率稳定度不高,可采用PLL频偏器进行改进
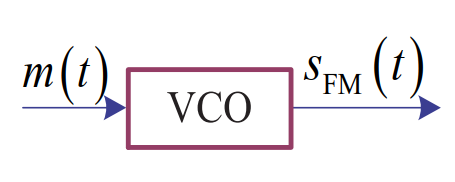
间接法
原理:积分→调相(NBFM)→n次倍频→WBFM
优点:频率稳定度好
缺点:需要多次倍频和混频,因此电路较复杂

调频信号的解调
非相干解调——鉴频器
适用:NBFM和WBFM
思路:完成频率~电压的转换,即
SFM(t)=Acos[ωct+Kf∫m(τ)dτ]→m0(t)∝Kfm(t)
一种振幅鉴频器如图
原理:
 SFM(t)=Acos[ωct+Kf∫m(τ)dτ]
SFM(t)=Acos[ωct+Kf∫m(τ)dτ]微分器:把幅度恒定的调频波变成调幅调频波
Sd(t)=−A[ωc+Kfm(t)]sin[ωct+Kf∫m(τ)dτ]包络检波器:检出包络并滤去直流,经LPF即得解调输出
m0(t)=KdKfm(t)式中,Kd为鉴频器灵敏度。
相干解调
仅适用于NBFM
5.3.5 调频信号的特点、优势和应用
包络稳定
频偏随调制信号m(t)作线性变化
相偏随消息信号m(t)的积分作线性变化
带宽与m(t)的带宽和mf有关,比AM带宽大(mf+1)倍
优势:抗噪声能力强
代价:占有较大的信道带宽,因而频率利用率较低
应用:要求高质量或信道噪声大的场合,例如:调频广播,电视伴音,卫星通信,移动通信,微波通信和蜂窝电话等系统
5.4 调频系统的抗噪声性能
分析方法和线性调制系统相似,解调器变为鉴频器,如图
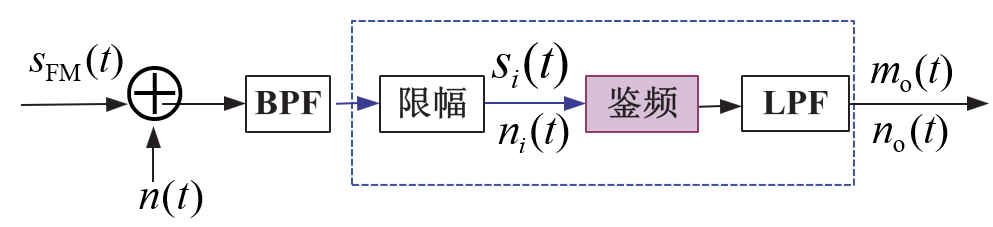
已知:
大信噪比时
若为单音调制,则
GFM=3mf2(mf+1)BFM=2(mf+1)fm=2(Δf+fm)可见:FM系统可通过增加传输带宽来改善抗噪声性能
注意:以带宽换取信噪比改善并不是永无止境的
小信噪比时:门限效应
5.5 各种模拟调制系统的比较
所有系统在同等条件下比较:
解调器输入信号功率为Si
信道噪声均值为0,单边带功率谱密度为0
基带信号带宽为fm
其中AM的调幅度为100%,正弦调制信号
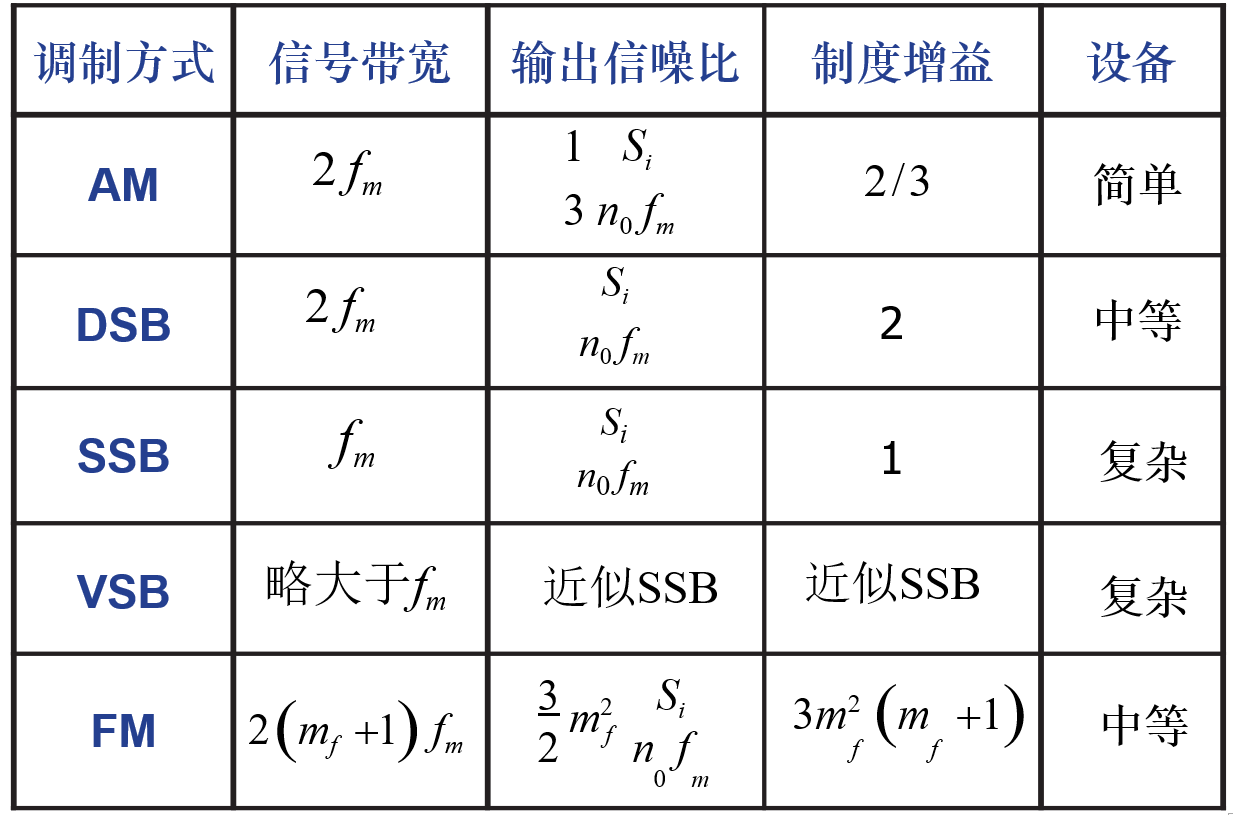
性能比较:
抗噪声性能:FM最好,DSB/SSB、VSB次之,AM最差
频谱利用率:SSB最高,VSB较高,DSB/AM次之,FM最差
功率利用率:FM最高,DSB/SSB、VSB次之,AM最差
设备复杂度:AM最简单,DSB/FM次之,VSB较复杂,SSB最复杂
特点与应用:
AM: 优点是接收设备简单;缺点是功率利用率低,抗干扰能力差。主要用在中波和短波调幅广播
DSB:优点是功率利用率高,带宽与AM相同。主要用于调频立体声中的差信号调制,彩色TV中的色差信号调制
SSB: 优点是功率利用率和频带利用率都较高,抗干扰能力和抗选择性衰落能力均优于AM,而带宽只有AM的一半;缺点是收发设备都复杂。常用于频分多路复用系统中
VSB: 抗噪声性能和频带利用率与SSB相当。在电视广播等系统中得到了广泛应用
FM: 抗干扰能力强,广泛应用于长距离高质量的通信系统 中。缺点是频带利用率低,存在门限效应
5.6 频分复用
频分:按照频率划分信道的复用方式
方法:调制→合成→传输→分路→解调
原理如图
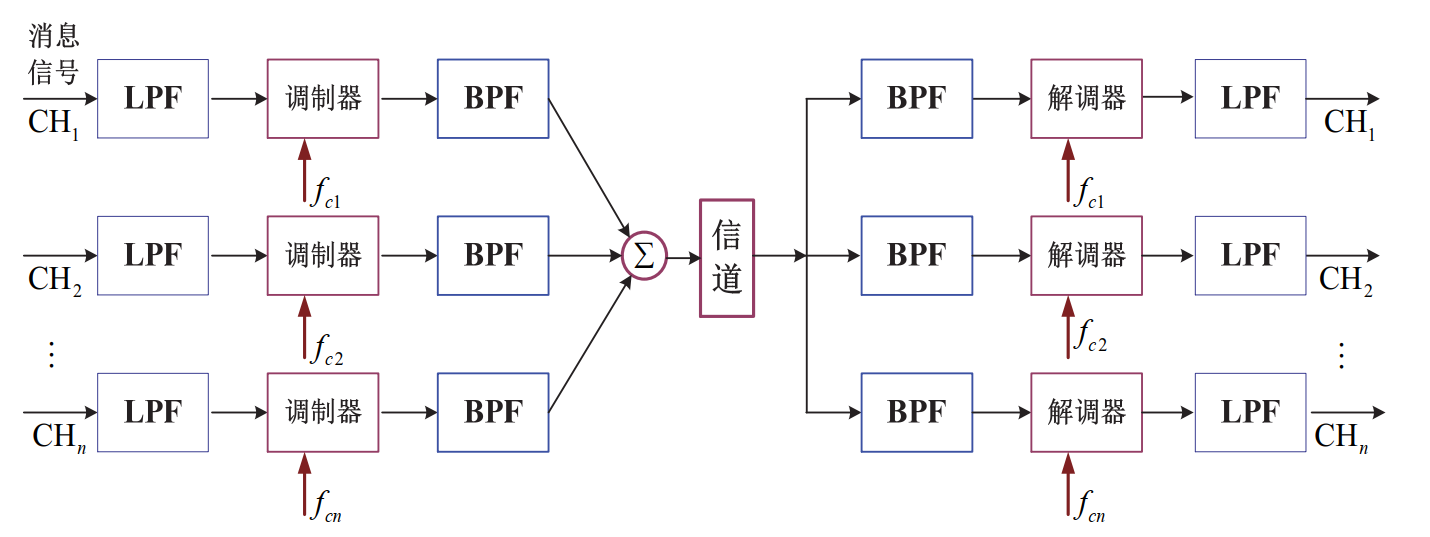
Last updated
