📓1. 熵和互信息

1.1 信息的介绍

信息论由克劳德·香农（Claude E. Shannon，1916-2001）通过《通信的数学理论》（A Mathematical Theory of Communication），发表于1948年《贝尔系统技术期刊》创立。

什么是信息？一些观察如下：

1. 信息源自不确定性。

2. 信息应与可能性的数量相关。

3. 信息应具有“可加性”。

4. 我们可以使用对数来缩小大量的可能性。

5. 二进制排列用于表示所有的可能性。

6. 信息的度量应考虑各种可能事件的概率。

因此，信息是：接收者未知的知识，是对不确定性的度量。

定义：给定消息 $M_1, M_2, . . . , M_q$，其发生的概率为 $P_1, P_2, . . . , P_q(P_1+P_2+...+P_q=1)$，则每条消息所携带的信息量的度量为

$$I(M_i)=\log_xP_i^{-1},\quad i=1,2,...,q$$

1. $x=2,:I(M_i)$单位是$bit$(比特)

2. $x=e,:I(M_i)$单位是$nats$(奈特)

3. $x=10,:I(M_i)$单位是$Hartley$(哈特莱)

信息量的性质：

1. 当 $P_i \to 1$ 时，$I(M_i) \to 0$；
2. 当 $0 \leq P_i \leq 1$ 时，$I(M_i) \geq 0$；
3. 如果 $P_j > P_i$，则 $I(M_i) > I(M_j)$；
4. 若 $M_i$ 和 $M_j$ 统计独立，则 $I(M_i\&M_j)=I(M_i)+I(M_j)$

1.2 熵

给定长度为 $N$ 的源向量。它有 $U$ 个可能的符号 $S_1, S_2,...,S_U$，每个符号出现的概率分别为 $P_1,P_2,...,P_U$。要表示该源向量，我们需要

$$I=\sum_{i=1}^UNP_i\log_2P_i^{-1}\mathrm{~bits}$$

平均而言，

$$H=\frac IN=\sum_{i=1}^UP_i\log_2P_i^{-1}\text{ bits/symbol}$$

$H$ 称为源熵，表示每个源符号的平均信息量。它也可以理解为函数 $\log_2P_i^{-1}$ 的期望值：

$$H=\mathbb{E}\left[\log_2P_i^{-1}\right]\text{bits/symbol}$$

不同底数的熵可以通过以下方式互换：

$$H_b(x)=H_a(x)\log_ba$$

证明如下：

$$\begin{align*} H_a(x)&=\mathbb{E}[-\log_aP(x)] \\ H_a(x)\log_ba &=\frac{\lg a}{\lg b}\mathbb{E}\left[-\frac{\lg P(x)}{\lg a}\right] \\ &=\mathbb{E}\left[-\frac{\lg P(x)}{\lg b}\right] \\ &=\mathbb{E}[-\log_bP(x)] \\ &=H_b(x) \end{align*}$$

现在我们考虑两个随机变量 $X$ 和 $Y$ 的熵，$X$ 和 $Y$ 的取值分别为 $x$ 和 $y$。$X$和 $Y$ 的分布分别为 $P(x)$ 和 $P(y)$。因此我们有：

联合熵 $H(X,Y)$：给定联合分布$P(x,y)$

$$H(X,Y)=-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(x,y) \\ =-\mathbb{E}[\log_2P(x,y)] \\$$

条件熵 $H(Y|X)$：

$$\begin{align} H(Y|X)&=\sum_{x\in X}P(x)H(Y|X=x) \\ &=-\sum_{x\in X}\sum_{y\in Y}P(x)P(y|x)\mathrm{log}_2P(y|x) \\ &=-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(y|x)=-\mathbb{E}[\mathrm{log}_2P(y|x)] \end{align}$$

链式法则（联合熵与条件熵的关系）：

$$\begin{aligned}H(X,Y)&=H(X)+H(Y|X)\\&=H(Y)+H(X|Y)\end{aligned}$$

证明如下：

$$\begin{aligned} H(X,Y)&=-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(x,y)\\&=-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2(P(y|x)P(x)) \\ &=-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(x)-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(y|x) \\ &=-\sum_{x\in X}P(x)\log_2P(x)-\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(y|x) \\ &=H(X)+H(Y|X) \end{aligned}$$

如果 $X$ 和 $Y$ 独立：

$$H(X|Y)=H(X)$$

因此

$$H(X,Y)=H(X)+H(Y)$$

该链式法则可以推广为：

$$\begin{aligned}&(1)~H(X,Y|Z)=H(X|Z)+H(Y|X,Z)\\&(2)~H(X_1,X_2,...,X_N)=\sum_{i=1}^NH(X_i|X_{i-1},X_{i-2},...,X_1)\end{aligned}$$

1.3 互信息

我们有两个随机变量 $X$ 和 $Y$，$X$ 和 $Y$ 的取值分别为 $x$ 和 $y$。$X$ 和 $Y$ 的分布分别为 $P(x)$ 和 $P(y)$。$X$ 和 $Y$ 的联合分布为 $P(x, y)$。

互信息 $I(X,Y)$ 的定义为：

$$\begin{aligned} I(X,Y)&=\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2\frac{P(x|y)}{P(x)}\\ &=\mathbb{E}\left[\log_2\frac{P(x|y)}{P(x)}\right] \end{aligned}$$

由以下关系可知：

$$\frac{P(x|y)}{P(x)}=\frac{P(x,y)}{P(x)P(y)}$$

因此：

$$I(X,Y)= \sum_{x\in X}\sum_{y\in Y}P(x,y)\log_2\frac{P(x,y)}{P(x)P(y)} =\mathbb{E}\left[\log_2\frac{P(x,y)}{P(x)P(y)}\right]$$

注意：如果 $X$ 和 $Y$ 独立，$P(x)P(y)=P(x,y)$，则 $I(X,Y)=0$。

互信息与熵的关系：

$$I(X,Y)=H(X)+H(Y)-H(X,Y)$$

证明如下：

$$\begin{aligned} I(X,Y)& =\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2\frac{P(x,y)}{P(x)P(y)} \\ &=\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2P(x,y)-\sum_{x\in X}P(x)\mathrm{log}_2P(x)-\sum_{y\in Y}P(y)\mathrm{log}_2P(y) \\ &=H(X)+H(Y)-H(X,Y) \end{aligned}$$

该证明还表明了互信息的对称性：

$$I(X,Y)=I(Y,X)$$

该关系也可以通过维恩图可视化表示。

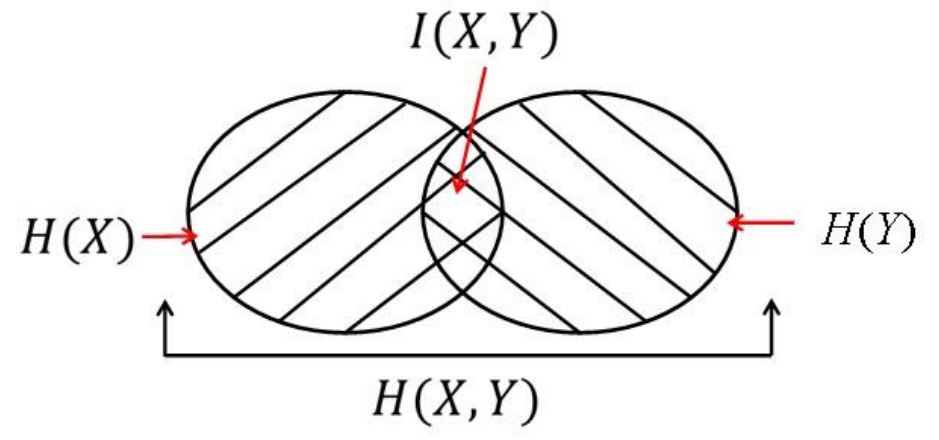
推论：

$$\begin{aligned}I(X,Y)&=H(X)-H(X|Y)\\&=H(Y)-H(Y|X)\end{aligned}$$

结论如下：

1. $0\leq I(X,Y)\leq\min{H(X),H(Y)}$；
2. 如果 $H(X)\subset H(Y)$，则 $I(X,Y)=H(X)$。类似地，如果 $H(Y)\subset H(X)$，则 $I(X,Y)=H(Y)$；
3. $I(X,X)=H(X)-H(X|X)=H(X)$，熵也称为自信息。

对于互信息，任意多个变量的链式法则如下：

$$\begin{aligned} I(X_1,X_2,...,X_N;Y)& =H(X_1,X_2,...,X_N)-H(X_1,X_2,...,X_N|Y) \\ &=\sum_{i=1}^NH(X_i|X_1,X_2,...,X_{i-1})-\sum_{i=1}^NH(X_i|X_1,X_2,...,X_{i-1},Y) \\ &=\sum_{i=1}^NH(X_i|X_1,X_2,...,X_{i-1})-H(X_i|X_1,X_2,...,X_{i-1},Y) \\ &=\sum_{i=1}^NI(X_i;Y|X_1,X_2,...,X_{i-1}) \end{aligned}$$

假设 $X$ 是传输信号，$Y$ 是接收信号。

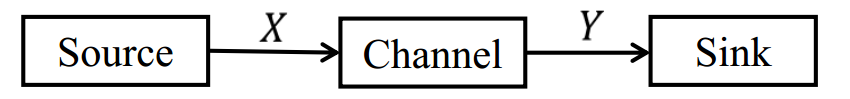
互信息 $I(X, Y)$ 描述了一个变量 $X$ 包含关于另一个变量 $Y$ 的信息量，或反过来为 $I(Y, X)$。

1.4 信息论的进一步结果

相对熵：假设 $X$ 和 $\widehat{X}$ 是两个随机变量，取值分别为 $x$ 和 $\widehat{x}$。它们旨在描述同一事件，其概率质量函数分别为 $P(x)$ 和 $P(\hat{x})$。它们的相对熵定义为：

$$\begin{aligned}D\big(P(x),P(\hat{x})\big)&=\sum_{x\in\operatorname{supp}P(x)}P(x)\mathrm{log}_2\frac{P(x)}{P(\hat{x})}\\&=\mathbb{E}\left[\log_2\frac{P(x)}{P(\hat{x})}\right]\\\end{aligned}$$

• 相对熵通常称为两个分布 $P(x)$ 和 $P(\widehat{x})$ 之间的 Kullback-Leibler（KL 距离）。

  当假设分布为 $P(\hat{x})$ 而真实分布为 $P(x)$ 时，它是一种低效性的度量。例如，事件可以用平均长度为 $H(P(x))$ 位描述。然而，如果我们假设其分布为 $P(\widehat{x})$，我们需要平均长度为 $H( P( x) ) + D\left ( P( x) , P( \hat{x} ) \right )$ 位来描述它。

  它不是对称的，即 $D(P(x),P(\hat{x}))\neq D\left(P(\hat{x}),P(x)\right)$。

推论 1：

$$\text{When }P(x)=P(\hat{x}),D\Big(P(x),P(\hat{x})\Big)=0.$$

推论 2：

$$D\big(P(x),P(\hat{x})\big) \ge 0$$

证明如下：

$$\begin{aligned} -D\big(P(x),P(\hat{x})\big)& =\sum_{x\in\operatorname{supp}P(x)}P(x)\log_2\frac{P(\hat{x})}{P(x)} \\ &\leq\sum_{x\in\operatorname{supp}P(x)}P(x)\left(\frac{P(\hat{x})}{P(x)}-1\right)\log_2e \\ &=\left(\sum_{x\in\operatorname{supp}P(x)}P(\hat{x})-\sum_{x\in\operatorname{supp}P(x)}P(x)\right)\log_2e \\ &\leq(1-1)\mathrm{log}_2e \\ &=0 \end{aligned}$$

凸函数：若函数 $f(x)$ 在区间 $(a,b)$ 上是凸的，即对于 $x_{1},x_{2}\in(a,b)$ 且 $0\leq\lambda\leq1$，有：

$$f(\lambda x_{1}+(1-\lambda)x_{2})\leq\lambda f(x_{1})+(1-\lambda)f(x_{2})$$

当且仅当 $\lambda=0$ 或 $\lambda=1$ 时，等号成立，则该函数为严格凸函数。

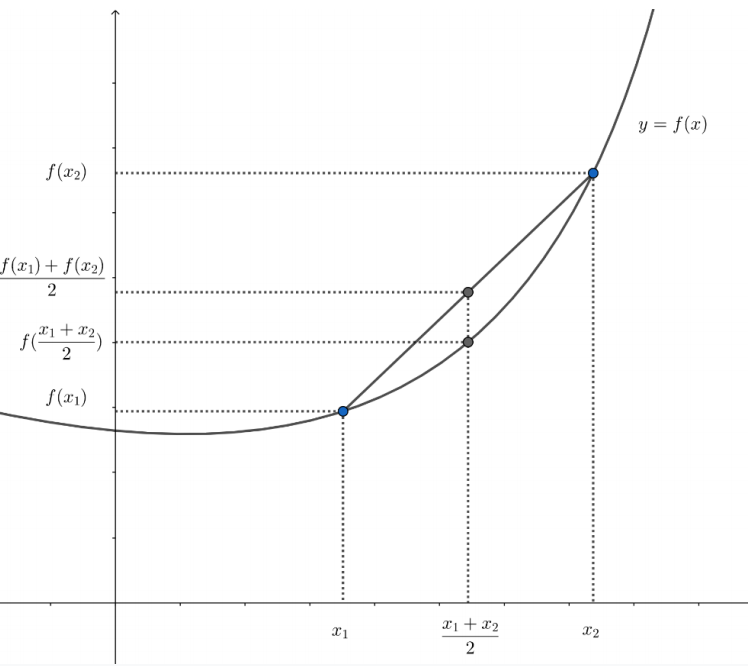
如果 $f(x)$ 是凸函数，则 $-f(x)$ 是凹函数。

詹森不等式：如果函数 $f(x)$ 是凸的，则有：

$$f(\mathbb{E}[x])\leq\mathbb{E}[f(x)]$$

詹森不等式可以用于证明一些关于熵的性质。

推论 2: $D\big(P(x),P(\hat{x})\big) \ge 0$

$$\begin{aligned}-D\big(P(x),P(\hat{x})\big)&=\sum_{x\in\operatorname{supp}P(x)}P(x)\log_2\frac{P(\hat{x})}{P(x)}\\&\leq\log_2\sum_{x\in\operatorname{supp}P(x)}P(\hat{x})\\&\leq\log_21=0\end{aligned}$$

推论 3: $I( X, Y) \geq 0$

$$\begin{aligned}I(X,Y)&=\sum_{x\in X}\sum_{y\in Y}P(x,y)\mathrm{log}_2\frac{P(x,y)}{P(x)P(y)}\\&=D(P(x,y),P(x)P(y))\geq0\end{aligned}$$

仅当 $P(x,y)=P(x)P(y)$ 时，$I(X,Y)=0$，即 $X$ 和 $Y$ 独立。

推论 4（最大熵分布）：

给定变量 $X\in{x_1,x_2,...,x_U}$，其分布为 $P_1,P_2,...,P_U$。我们有：

$$H(X)\leq\log_2U$$

证明：

由于 $\log_2(\cdot)$ 是一个凹函数，基于詹森不等式，我们有：

$$\begin{aligned}H(X)&\leq\log_2\left(\sum_{i=1}^UP_iP_i^{-1}\right)\\&=\log_2U\end{aligned}$$

注意：如果 $X$ 在 $x_1, x_2, . . . , x_U$ 上均匀分布，即 $P_1= P_2= \cdots = P_U= \frac 1U$，则有：

$$H(X)=\log_2U$$

费诺不等式：设 $X$ 和 $Y$ 是两个随机变量，其取值来自 ${x_1,x_2,...x_k}$。设 $P_e=\Pr[X\neq Y]$，则有：

$$H(X|Y)\leq H(P_e)+P_e\log_2(k-1).$$

证明：我们构造一个二元变量 $Z$得：

$$\begin{aligned} &Z=0,\operatorname{if}X=Y \\&Z=1,\operatorname{if}X\neq Y \end{aligned}$$

因此

$$\begin{aligned}&\Pr(Z=0)=1-P_e\\&\Pr(Z=1)=P_e\end{aligned}$$

因此，$H(Z)=H(P_e)$。基于熵的链式法则：

$$H(XZ|Y)=H(X|Y)+H(Z|XY)=H(X|Y)$$

注意，已知 $X$ 和 $Y$ 时，$Z$ 是确定的，且 $H(Z|XY)=0$。同样基于链式法则：

$$\begin{align} H(XZ|Y)&=H(Z|Y)+H(X|YZ)\\ &\leq H(Z)+H(X|YZ) \end{align}$$

因此

$$\begin{aligned} H(X|YZ)& =\Pr(Z=0) H(X|Y,Z=0)+\Pr(Z=1) H(X|Y,Z=1). \\ &=(1-P_e)\cdot0+P_e\log_2(k-1) \\ &=P_e\log_2(k-1) \end{aligned}$$

注意：$H(P_e)$ 是在 $X=Y$ 时描述 $X$ 所需的比特数；$\log_2(k-1)$ 是在 $X\neq Y$ 时描述 $X$ 所需的比特数。当 $X$ 在所有 $k-1$ 个值上均匀分布时，等号成立。

信息处理不等式：给定一个串联的数据处理系统：

马尔可夫链 $X\to Y\to Z$ 表示在给定 $Y$ 的情况下，$X$ 和 $Z$ 条件独立，因此有以下关系：

$$P(z|x,y)=P(z|y)\\ P(x|y,z)=P(x|y)$$

因此我们有

$$P(x,y,z)=P(x,y)\cdot P(z|y)=P(x)P(y|x)P(z|y)$$

得

$$I(X,Z)\leq\begin{cases}&I(X,Y)\\&I(Y,Z)\end{cases}$$

证明：

$$\begin{aligned} I(X,{Z})& =H(X)-H(X|Z) \\ &\leq H(X)-H(X|ZY) \\ &=H(X)-H(X|Y) \\ &=I(X,Y) \end{aligned}$$

数据处理无法增加信息。